Cho hình 43. Chứng minh AI = IM ?
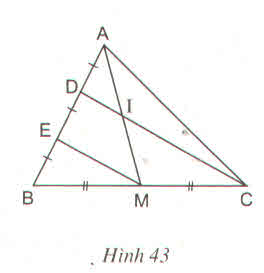
Cho hình 43. Chứng minh AI = IM ?

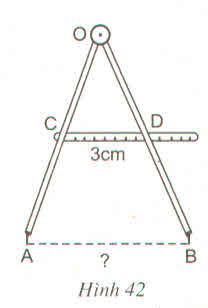
Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết C là trung điểm của OA, D là trung điểm của OB và CD = 3 cm
Thảo luận (3)Hướng dẫn giảiBài giải:
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = 1212AB
Suy ra AB = 2CD = 2.3 = 6cm.
(Trả lời bởi Hiiiii~)
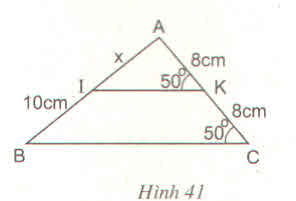
Tính x trên hình 41 :
Thảo luận (3)Hướng dẫn giảiBài giải:
Ta có
=
= 500 nên IK // BC (
=
(đồng vị)
Mà KA = KC suy ra IA = IB = 10cm
Vậy x = 10cm
(Trả lời bởi Hiiiii~)