Tính x trên hình 41 :
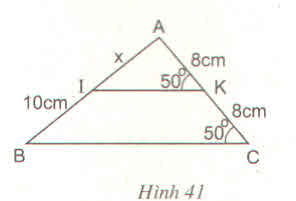
Tính x trên hình 41 :

Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết C là trung điểm của OA, D là trung điểm của OB và CD = 3 cm
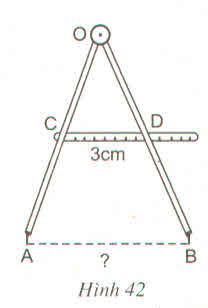
Thảo luận (3)Hướng dẫn giảiBài giải:
Ta có CO = CA (gt)
DO = DB (gt)
Nên CD là đường trung bình của ∆OAB.
Do đó CD = 1212AB
Suy ra AB = 2CD = 2.3 = 6cm.
(Trả lời bởi Hiiiii~)
Cho hình 43. Chứng minh AI = IM ?
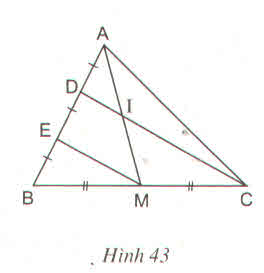
Thảo luận (2)Hướng dẫn giải∆BDC có BE = ED và BM = MC
nên EM // DC
==> DI // EM
∆AEM có AD = DE và DI // EM
==> AI = IM.
(Trả lời bởi Linh Phương)
Tính x trên hình 44
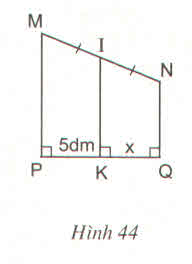
Thảo luận (1)Hướng dẫn giảiBài giải:
Ta có IM = IN, IK // MP // NQ
nên K là trung điểm của PQ.
Do đó PK = KQ = 5
Vậy x = 5dm.
(Trả lời bởi Hiiiii~)
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20 cm. Tính khoảng cách từ trung điểm C của AB đến xy ?
Thảo luận (1)Hướng dẫn giải
Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng ?
Thảo luận (3)Hướng dẫn giảiBài giải:
Ta có EA = ED, KB = KD (gt)
Nên EK // AB
Lại có FB = FC, KB = KD (gt)
Nên KF // DC // AB
Qua K ta có KE và KF cùng song song với AB nên theo tiên đề Ơclit ba điểm E, K, F thẳng hàng.
(Trả lời bởi Hiiiii~)
Tính x, y trên hình 45, trong đó AB // CD // EF // GH
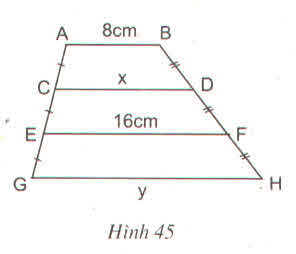
Thảo luận (1)Hướng dẫn giảiBài giải:
AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE.
Do đó: CD = \(\dfrac{AB+EF}{2}\) = \(\dfrac{8+16}{2}\) = 12
Hay x = 12
Tương tự CDHG là hình thang, EF là đường trung bình của hình thang CDHG.
Nên EF = \(\dfrac{CD+GH}{2}\) => GH = 2EF -CD = 2.16 - 12
GH = 20 hay y = 20
Vậy x = 12, y = 20
(Trả lời bởi Hiiiii~)
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC
a) So sánh độ dài EK và CD, KF và AB
b) Chứng minh rằng \(EF\le\dfrac{AB+CD}{2}\)
Thảo luận (2)Hướng dẫn giải
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
(Trả lời bởi Hương Yangg)
Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD ở I, cắt AC ở K
a) Chứng minh rằng AK = KC, BI = ID
b) Cho AB = 6cm, CD = 10 cm. Tính các độ dài EI, KF, IK ?
Thảo luận (2)Hướng dẫn giảia) Vì EA = ED, FB = FC (gt)
Nên EF là đường trung bình của hình thang ABCD.
Do đó: EF // AB // CD
∆ABC có BF = FC và FK // AB
nên: AK = KC
∆ABD có AE = ED và EI // AB
nên: BI = ID
b) Vi EF là đường trung bình của hình thang ABCD.
nên EF = \(\dfrac{AB+CD}{2}\) = \(\dfrac{6+10}{2}=8\)
EI là đường trung bình của ∆ABD nên \(EI=\dfrac{1}{2}AB=\dfrac{1}{2}.6=3\left(cm\right)\)
KF là đường trung bình của ∆ABC nên \(KF=\dfrac{1}{2}AB=\dfrac{1}{2}.6=3\left(cm\right)\)
Lại có EF = EI + IK + KF
nên IK = EF - (EI + KF) = 8 - (3 + 3) = 2 (cm)
(Trả lời bởi BW_P&A)
Cho tam giác ABC, điểm D thuộc cạnh AC sao cho \(AD=\dfrac{1}{2}DC\). Gọi M là trung điểm của BC, I là giao điểm của BD và AM.
Chứng minh rằng AI = IM ?
Thảo luận (3)Hướng dẫn giảiTa gọi E là trung điểm của DC
Vì tam giác ABC có
BM = MC
DE = EC
=> BD // ME
=> DI // ME
mà tâm giac ADE có AD = DE và DI // ME nên AI = IM (đpcm)
(Trả lời bởi a2tralan lynguyen)