Vị trí của Mặt Trời so với đường chân trời (Hình 19) gợi nên hình ảnh vị trí tương đối của đường thẳng và đường tròn.
Làm thế nào để xác định được vị trí tương đối của đường thẳng và đường tròn?
Bài 2. Vị trí tương đối của đường thẳng và đường tròn
Khởi động (SGK Cánh Diều - Tập 1 - Trang 101)
Thảo luận (1)
Hoạt động 1 (SGK Cánh Diều - Tập 1 - Trang 101)
Quan sát Hình 20.
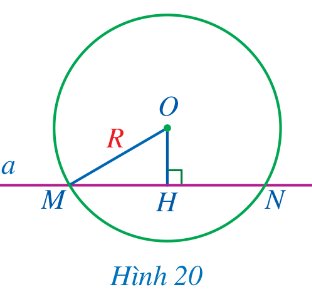
a) Cho biết đường thẳng a và đường tròn (O; R) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng OH và R.
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) có 2 điểm chung.
b) Xét tam giác \(OMH\) vuông tại \(H\) có: \(OH\) là cạnh góc vuông, \(OM\) là cạnh huyền.
Nên \(OH < OM\) lại có \(OM = R\). Vậy \(OH < R\).
(Trả lời bởi datcoder)
Luyện tập 1 (SGK Cánh Diều - Tập 1 - Trang 102)
Hãy chỉ ra một số hiện tượng trong thực tiễn gợi nên hình ảnh của đường thẳng và đường tròn cắt nhau.
Thảo luận (1)Hướng dẫn giảiMột số hiện tượng trong thực tiễn gợi nên hình ảnh của đường thẳng và đường tròn cắt nhau: biển báo giao thông (chẳng hạn biển cấm đường), đĩa có họa tiết kẻ caro, …
(Trả lời bởi datcoder)
Hoạt động 2 (SGK Cánh Diều - Tập 1 - Trang 102)
Trong bức ảnh ở Hình 22, đường ray và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?
Thảo luận (1)Hướng dẫn giảiĐường thẳng và đường tròn tiếp xúc nhau có 1 điểm chung
(Trả lời bởi datcoder)
Luyện tập 2 (SGK Cánh Diều - Tập 1 - Trang 102)
Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Đường thẳng AB có tiếp xúc với đường tròn (C; 4 cm) hay không? Vì sao?
Thảo luận (1)Hướng dẫn giải
Xét tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pythagore ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow {3^2} + A{C^2} = {5^2} \Rightarrow AC = 4\left( {cm} \right)\).
Vậy đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\).
(Trả lời bởi datcoder)
Hoạt động 3 (SGK Cánh Diều - Tập 1 - Trang 103)
Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?
Thảo luận (1)Hướng dẫn giảiĐường thẳng và đường tròn không giao nhau không có điểm chung.
(Trả lời bởi datcoder)
Hoạt động 4 (SGK Cánh Diều - Tập 1 - Trang 103)
Quan sát Hình 26.
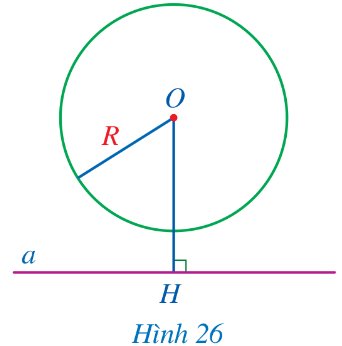
a) Cho biết đường thẳng a và đường tròn (O; R) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng OH và R.
Thảo luận (1)Hướng dẫn giảia) Đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) không có điểm chung.
b) \(OH > R\).
(Trả lời bởi datcoder)
Luyện tập 3 (SGK Cánh Diều - Tập 1 - Trang 104)
Cho điểm O và đường thẳng a thỏa mãn khoảng cách từ O đến đường thẳng a bằng 4 cm. Xác định vị trí tương đối của đường thẳng a và các đường tròn (O; 3 cm), (O; 4 cm), (O; 5 cm).
Thảo luận (1)Hướng dẫn giảiKhoảng cách từ \(O\) đến đường thẳng \(a\) bằng 4cm \( \Rightarrow d = 4\left( {cm} \right)\).
+ Với đường tròn \(\left( {O;3cm} \right)\) ta có: \(4 > 3 \Rightarrow d > R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;3cm} \right)\) không giao nhau.
+ Với đường tròn \(\left( {O;4cm} \right)\) ta có: \(4 = 4 \Rightarrow d = R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;4cm} \right)\) tiếp xúc nhau.
+ Với đường tròn \(\left( {O;5cm} \right)\) ta có: \(4 < 5 \Rightarrow d < R\).
Vậy đường thẳng \(a\) và đường tròn \(\left( {O;5cm} \right)\) cắt nhau.
(Trả lời bởi datcoder)
Bài tập 1 (SGK Cánh Diều - Tập 1 - Trang 104)
Đồng hồ treo tường trang trí ở Hình 29 gợi nên vị trí tương đối của đường thẳng và đường tròn.
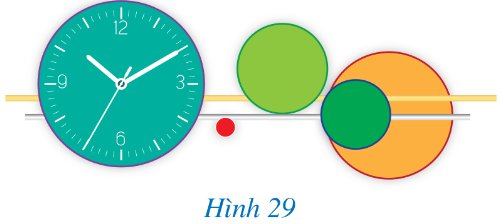
Quan sát Hình 29 và chỉ ra một hình ảnh đường thẳng và đường tròn:
a) Cắt nhau;
b) Tiếp xúc nhau;
c) Không giao nhau.
Thảo luận (1)Hướng dẫn giảia) Cắt nhau: Đường tròn xanh lá cây to với đường thẳng màu vàng.
b) Tiếp xúc nhau: Đường tròn xanh lá cây to với đường thẳng màu trắng.
c) Không giao nhau: Đường tròn xanh lá cây nhỏ với đường thẳng màu vàng.
(Trả lời bởi datcoder)
Bài tập 2 (SGK Cánh Diều - Tập 1 - Trang 104)
Trong Hình 30, mép ngoài cửa ra vào có dạng một phần của đường tròn bán kính 1,6 m. Hãy tính chiều cao HK của cửa đó (làm tròn kết quả đến hàng phần mười của mét), biết AH = 0,9 m.
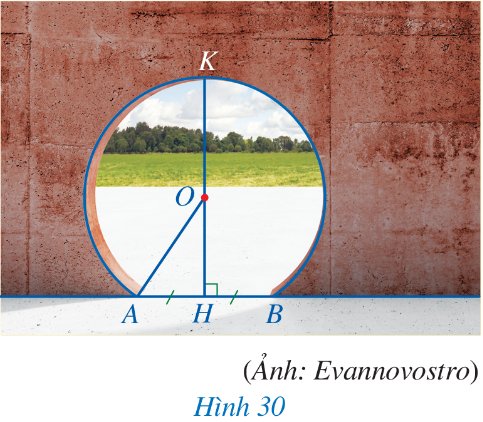
Thảo luận (1)Hướng dẫn giảiÁp dụng định lý Pythagore vào tam giác \(AOH\) vuông tại \(H\), ta có:
\(A{O^2} = O{H^2} + A{H^2} \\ 1,{6^2} = O{H^2} + 0,{9^2} \\ OH = \frac{{\sqrt 7 }}{2}\left( m \right)\)
Chiều cao \(HK\) của cửa đó là: \(HK = OK + OH = 1,6 + \frac{{\sqrt 7 }}{2} \approx 2,9\left( m \right)\).
(Trả lời bởi datcoder)