Tính các tích phân sau:
a) \(\int\limits^4_{-2}\left(x+1\right)\left(x-1\right)dx;\) b) \(\int\limits^2_1\dfrac{x^2-2x+1}{x}dx;\) c) \(\int\limits^{\dfrac{\pi}{2}}_0\left(3\sin x-2\right)dx;\) d) \(\int\limits^{\dfrac{\pi}{2}}_0\dfrac{\sin^2x}{1+\cos x}dx.\)
Giả sử tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t (giây) được cho bởi công thức:
\(\left\{{}\begin{matrix}t,\text{ }0\le t\le2,\\2,\text{ }2< t\le20,\\12-0,5t,\text{ }20< t\le24.\end{matrix}\right.\)
Tính quãng đường chuyển động và tốc độ trung bình của thang máy.
Thảo luận (1)Hướng dẫn giảiGọi \(s\left( t \right)\) là quãng đường thang máy di chuyển được đến thời gian \(t\) (giây).
Quãng đường thang máy di chuyển từ tầng 1 lên tầng cao nhất là \(s = s\left( {20} \right) - s\left( 0 \right) = \int\limits_0^{20} {v\left( t \right)dt} = \int\limits_0^2 {v\left( t \right)dt} + \int\limits_2^{20} {v\left( t \right)dt} + \int\limits_{20}^{24} {v\left( t \right)dt} \)
\( = \int\limits_0^2 {tdt} + \int\limits_2^{20} {2dt} + \int\limits_{20}^{24} {\left( {12 - 0,5t} \right)dt} = \left. {\left( {\frac{{{t^2}}}{2}} \right)} \right|_0^2 + 2\left. {\left( t \right)} \right|_2^{20} + \left. {\left( {12t - \frac{{0,5{t^2}}}{2}} \right)} \right|_{20}^{24}\)
\( = \left( {2 - 0} \right) + 2\left( {20 - 2} \right) + \left( {144 - 140} \right) = 42{\rm{ }}\left( {\rm{m}} \right)\).
Vận tốc trung bình của thang máy là \({v_{tb}} = \frac{s}{t} = \frac{{42}}{{24}} = 1,75\left( {{\rm{m/s}}} \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Một ô tô đang di chuyển với vận tốc 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức v(t) = 20 – 5t (0 ≤ t ≤ 4).
Kể từ khi hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?
Tính các tích phân sau:
a) \(\int\limits^1_{-2}\left|2x+2\right|dx;\) b) \(\int\limits^4_0\left|x^2-4\right|dx;\) c) \(\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\left|\sin x\right|dx\).
Thảo luận (1)Hướng dẫn giảia) \(\int\limits_{ - 2}^1 {\left| {2x + 2} \right|dx} = \int\limits_{ - 2}^{ - 1} {\left| {2x + 2} \right|dx} + \int\limits_{ - 1}^1 {\left| {2x + 2} \right|dx} = \int\limits_{ - 2}^{ - 1} { - \left( {2x + 2} \right)dx} + \int\limits_{ - 1}^1 {\left( {2x + 2} \right)dx} \)
\( = - \left. {\left( {{x^2} + 2x} \right)} \right|_{ - 2}^{ - 1} + \left. {\left( {{x^2} + 2x} \right)} \right|_{ - 1}^1 = - \left[ {\left( { - 1} \right) - 0} \right] + \left[ {3 - \left( { - 1} \right)} \right] = 5\)
b) \(\int\limits_0^4 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^4 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left( {4 - {x^2}} \right)dx} + \int\limits_2^4 {\left( {{x^2} - 4} \right)dx} \)
\( = \left. {\left( {4x - \frac{{x{\rm{\^3}}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{x{\rm{\^3}}}}{3} - 4x} \right)} \right|_2^4 = \left( {\frac{{16}}{3} - 0} \right) + \left[ {\frac{{16}}{3} - \left( { - \frac{{16}}{3}} \right)} \right] = 16\)
c) \(\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left| {\sin x} \right|dx} = \int\limits_{ - \frac{\pi }{2}}^0 {\left| {\sin x} \right|dx} + \int\limits_0^{\frac{\pi }{2}} {\left| {\sin x} \right|dx} = \int\limits_{ - \frac{\pi }{2}}^0 {\left( { - \sin x} \right)dx} + \int\limits_0^{\frac{\pi }{2}} {\sin xdx} \)
\( = - \left. {\left( { - \cos x} \right)} \right|_{ - \frac{\pi }{2}}^0 + \left. {\left( { - \cos x} \right)} \right|_0^{\frac{\pi }{2}} = - \left[ { - 1 - 0} \right] + \left[ {0 - \left( { - 1} \right)} \right] = 2\)
(Trả lời bởi Nguyễn Quốc Đạt)
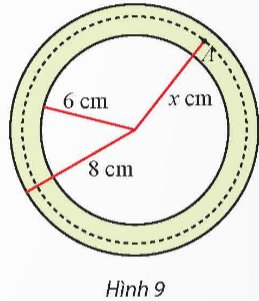
Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình 9. Khí bên trong ống được duy trì ở 150°C. Biết rằng nhiệt độ T(°C) tại điểm A trên thành ống là hàm số của khoảng cách x (cm) từ A đến tâm của mặt cắt và T′(x) = \(-\dfrac{30}{x}\) (6 ≤ x ≤ 8).
(Nguồn: Y.A.Cengel, A.I.Gahjar, Heat and Mass Transfer, McGraw Hill, 2015)
Tìm nhiệt độ mặt ngoài của ống.
Thảo luận (1)Hướng dẫn giảiDo nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\).
Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\).
Ta có \(\int\limits_6^8 {T'\left( x \right)dx} = \int\limits_6^8 { - \frac{{30}}{x}dx} = - 30\int\limits_6^8 {\frac{1}{x}dx = - 30.\left. {\left( {\ln \left| x \right|} \right)} \right|_6^8 = - 30\ln 8 + 30\ln 6} \).
Vậy nhiệt độ bên ngoài mặt ống là \(T\left( 8 \right) = - 30\ln 8 + 30\ln 6 + 150 \approx 141,{37^o}C\)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số y = f(x) = x + 1. Với mỗi x ≥ 1, kí hiệu S(x) là diện tích của hình thang giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng vuông góc với Ox tại các điểm có hoành độ 1 và x.
a) Tính S(3).
b) Tính S(x) với mỗi x ≥ 1.
c) Tính S'(x). Từ đó suy ra S(x) là một nguyên hàm của f(x) trên [1; +∞).
d) Cho F(x) là một nguyên hàm của hàm số f(x). Chứng tỏ rằng F(3) – F(1) = S(3). Từ đó nhận xét về cách tính S(3) khi biết một nguyên hàm của f(x).
Thảo luận (1)Hướng dẫn giải
a) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Dễ thấy rằng \(ABCD\) là hình thang vuông có hai đáy là \(AD\) và \(BC\), chiều cao là \(AB\).
Ta có \(AB = 3 - 1 = 2\), \(AD = 2\) và \(BC = 4\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( 3 \right) = \frac{{\left( {2 + 4} \right).2}}{2} = 6\).
b) Tương tự câu a, nhưng hoành độ của \(B\) là \(x\), ta suy ra tung độ của \(C\) là \(x + 1\).
Ta có \(AB = x - 1\), \(AD = 2\), \(BC = x + 1\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( x \right) = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2 + x + 1} \right)\left( {x - 1} \right)}}{2} = \frac{{\left( {x + 3} \right)\left( {x - 1} \right)}}{2} = \frac{{{x^2} + 2x - 3}}{2}\)
c) Ta có \(S'\left( x \right) = \frac{{2x + 2}}{2} = x + 1 = f\left( x \right)\). Vậy \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\).
d) Do \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\), ta có:
\(F\left( x \right) = \int {f\left( x \right)dx} = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C\)
Suy ra \(F\left( 3 \right) = \frac{{{3^2}}}{2} + 3 + C = \frac{{15}}{2} + C\) và \(F\left( 1 \right) = \frac{{{1^2}}}{2} + 1 + C = \frac{3}{2} + C\)
Như vậy ta có \(F\left( 3 \right) - F\left( 1 \right) = \left( {\frac{{15}}{2} + C} \right) - \left( {\frac{3}{2} + C} \right) = 6 = S\left( 3 \right)\).
Do đó, để tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\), ta thực hiện tính nguyên hàm \(F\left( x \right)\) của \(f\left( x \right)\), sau đó ta tính \(F\left( 3 \right)\) và \(F\left( 1 \right)\), từ đó tính được \(S\left( 3 \right) = F\left( 3 \right) - F\left( 1 \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = ex, trục hoành, trục tung và đường thẳng x = 1 (Hình 4).
Thảo luận (1)Hướng dẫn giảiTa có hàm số \(y = f\left( x \right) = {e^x}\) liên tục và dương trên đoạn \(\left[ {0;1} \right]\).
Ta có \(\int {f\left( x \right)dx} = \int {{e^x}dx} = {e^x} + C\), từ đó suy ra \(F\left( x \right) = {e^x}\) là một nguyên hàm của \(f\left( x \right) = {e^x}\).
Diện tích hình thang cong cần tính là: \(S = F\left( 1 \right) - F\left( 0 \right) = {e^1} - {e^0} = e - 1\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hàm số f(x) = 2x – 1. Lấy hai nguyên hàm tùy ý F(x) và G(x) của f(x), rồi tính F(3) – F(0) và G(3) – G(0). Nhận xét về kết quả nhận được.
Thảo luận (1)Hướng dẫn giảiTa có \(\int {f\left( x \right)dx} = \int {\left( {2x - 1} \right)dx} = {x^2} - x + C\)
Chọn \(F\left( x \right) = {x^2} - x\) và \(G\left( x \right) = {x^2} - x + 1\).
Ta có
\(F\left( 3 \right) - F\left( 0 \right) = \left( {{3^2} - 3} \right) - \left( {{0^2} - 0} \right) = 6\)
\(G\left( 3 \right) - G\left( 0 \right) = \left( {{3^2} - 3 + 1} \right) - \left( {{0^2} - 0 + 1} \right) = 6\)
Như vậy \(F\left( 3 \right) - F\left( 0 \right) = G\left( 3 \right) - G\left( 0 \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Tính các tích phân sau:
a) \(\int\limits^3_12xdx;\) b) \(\int\limits^{\pi}_0\sin tdt;\) c) \(\int\limits^{\ln2}_0e^udu.\)
Thảo luận (1)Hướng dẫn giảia) \(\int\limits_1^3 {2xdx} = \left. {{x^2}} \right|_1^3 = {3^2} - {1^2} = 8\)
b) \(\int\limits_0^\pi {\sin tdt} = \left. {\left( { - \cos t} \right)} \right|_0^\pi = \left( { - \cos \pi } \right) - \left( { - \cos 0} \right) = 2\)
c) \(\int\limits_0^{\ln 2} {{e^u}du} = \left. {{e^u}} \right|_0^2 = {e^2} - {e^0} = {e^2} - 1\)
(Trả lời bởi Nguyễn Quốc Đạt)
Sau khi xuất phát, ô tô di chuyển với tốc độ v(t) = 2t − 0,03t2 (0 ≤ t ≤ 10),
trong đó v(t) tính theo m/s, thời gian t tính theo giây với t = 0 là thời điểm xe xuất phát
.a) Tính quãng đường xe đi được sau 5 giây, sau 10 giây.
b) Tính tốc độ trung bình của xe trong khoảng thời gian t = 0 đến t = 10.
Thảo luận (1)Hướng dẫn giảia) Gọi \(s\left( t \right)\) (m) là quãng đường ô tô đi được sau \(t\) giây.
Ta có \(s\left( t \right)\) là nguyên hàm của \(v\left( t \right)\).
a) Quãng đường xe đi được sau 5 giây là
\(s\left( 5 \right) - s\left( 0 \right) = \int\limits_0^5 {v\left( t \right)dt} = \int\limits_0^5 {\left( {2t - 0,03{t^2}} \right)dt} = \left. {\left( {{t^2} - 0,01{t^3}} \right)} \right|_0^5\)
\( = \left( {{5^2} - 0,{{01.5}^3}} \right) - \left( {{0^2} - 0,{{01.0}^3}} \right) = 23,75\)
Quãng đường xe đi được sau 10 giây là
\(s\left( {10} \right) - s\left( 0 \right) = \int\limits_0^{10} {v\left( t \right)dt} = \int\limits_0^{10} {\left( {2t - 0,03{t^2}} \right)dt} = \left. {\left( {{t^2} - 0,01{t^3}} \right)} \right|_0^{10}\)
\( = \left( {{{10}^2} - 0,{{01.10}^3}} \right) - \left( {{0^2} - 0,{{01.0}^3}} \right) = 90\)
b) Tốc độ trung bình của xe trong khoảng thời gian từ \(t = 0\) đến \(t = 10\) là:
\({v_{tb}} = \frac{s}{t} = \frac{{90}}{{10}} = 9\)\(\left( {{\rm{m/s}}} \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)
