Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp: A = {0; 4; 8; 12; 16}
Bài 2: Tập hợp và các phép toán trên tập hợp
Bài 1.10 (SGK Kết nối tri thức với cuộc sống trang 19)
Thảo luận (1)
Bài 1.11 (SGK Kết nối tri thức với cuộc sống trang 19)
Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
\(A = \left\{ {x \in \mathbb{R}|\;{x^2} - 6 = 0} \right\}\);
\(B = \left\{ {x \in \mathbb{Z}|\;{x^2} - 6 = 0} \right\}\)
Thảo luận (1)Hướng dẫn giảiTa có: \({x^2} - 6 = 0 \Leftrightarrow x = \pm \sqrt 6 \in \mathbb{R}\)
Vì \(\sqrt 6 \in \mathbb{R}\) và \( -\sqrt 6 \in \mathbb{R}\) nên \( A = \left\{ { \pm \sqrt 6 } \right\}\)
Nhưng \( \pm \sqrt 6 \notin \mathbb{Z}\) nên không tồn tại \(x \in \mathbb{Z}\) để \({x^2} - 6 = 0\)
Hay \(B = \emptyset \).
(Trả lời bởi Hà Quang Minh)
Bài 1.12 (SGK Kết nối tri thức với cuộc sống trang 19)
Cho \(X = \left\{ {\,a\,;b} \right\}\). Các cách viết sau đúng hay sai? Giải thích kết luận đưa ra.
a) \(a \subset X\)
b) \(\left\{ a \right\} \subset X\);
c) \(\emptyset \in X\);
Thảo luận (1)Hướng dẫn giảia) Cách viết: \(a \subset X\) Sai vì \(\,a\) (là một phần tử của A) không phải là một tập hợp do đó ta phải dùng kí hiệu “\( \in \)” chứ không phải “\( \subset \)”.
Cách viết đúng: \(a \in X\)
b) Cách viết \(\left\{ a \right\} \subset X\) đúng, vì \(\left\{ a \right\}\)là một tập hợp, có duy nhất một phần tử là \(\,a\) và \(a \in X\)
=> Tập hợp \(\left\{ a \right\}\) là một tập con của \(X\).
c) Cách viết \(\emptyset \in X\) sai vì:
\(\emptyset \) là một tập hợp (tập hợp rỗng), không phải là một phần tử.
Cách viết đúng: \(\emptyset \subset X\)( Tập hợp rỗng là tập con của mọi tập hợp).
(Trả lời bởi Hà Quang Minh)
Bài 1.13 (SGK Kết nối tri thức với cuộc sống trang 19)
Cho \(A = \left\{ {2;5} \right\},\;\,B = \left\{ {5;x} \right\},\;\,C = \left\{ {2;y} \right\}\).Tìm \(x,y\) để \(A = B = C\).
Thảo luận (1)Hướng dẫn giảiĐể \(A = B\)
\(\begin{array}{l} \Leftrightarrow \left\{ {5;x} \right\} = \left\{ {2;5} \right\}\\ \Leftrightarrow x = 2\end{array}\)
Tương tự, ta có:
\(\begin{array}{l}A = C \\\Leftrightarrow \left\{ {2;y} \right\} = \left\{ {2;5} \right\} \\ \Leftrightarrow y = 5\end{array}\)
Vậy \(x = 2;y = 5\) thì \(A = B = C\).
(Trả lời bởi Hà Quang Minh)
Bài 1.14 (SGK Kết nối tri thức với cuộc sống trang 19)
Cho \(A = \left\{ {x \in \mathbb{Z}|\;x < 4} \right\},\) \( \,B = \left\{ {x \in \mathbb{Z}|\;\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0} \right\}\)
a) Liệt kê các phần tử của hai tập hợp A và B.
b) Hãy xác định các tập hợp \(A \cap B,A \cup B\) và \(A\,{\rm{\backslash }}\,B\)
Thảo luận (1)Hướng dẫn giảia) \(A = \{ 3;2;1;0; - 1; - 2; - 3; -4; ...\} \)
Tập hợp B là tập các nghiệm nguyên của phương trình \(\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0\)
Ta có:
\(\begin{array}{l}\left( {5x - 3{x^2}} \right)\left( {{x^2} + 2x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}5x - 3{x^2} = 0\\{x^2} + 2x - 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}x = 0\\x = \frac{5}{3}\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array} \right.\end{array}\)
Vì \(\frac{5}{3} \notin \mathbb Z\) nên \(B = \left\{ { - 3;0;1} \right\}\).
b) \(A \cap B = \left\{ {x \in A|x \in B} \right\} = \{ - 3;0;1\} = B\)
\(A \cup B = \) {\(x \in A\) hoặc \(x \in B\)} \( = \{ 3;2;1;0; - 1; - 2; - 3;...\} = A\)
\(A\,{\rm{\backslash }}\,B = \left\{ {x \in A|x \notin B} \right\} = \{ 3;2;1;0; - 1; - 2; - 3;...\} {\rm{\backslash }}\;\{ - 3;0;1\} = \{ 3;2; - 1; - 2; - 4; - 5; - 6;...\} \)
(Trả lời bởi Hà Quang Minh)
Bài 1.15 (SGK Kết nối tri thức với cuộc sống trang 19)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - 4;1] \cap [0;3)\)
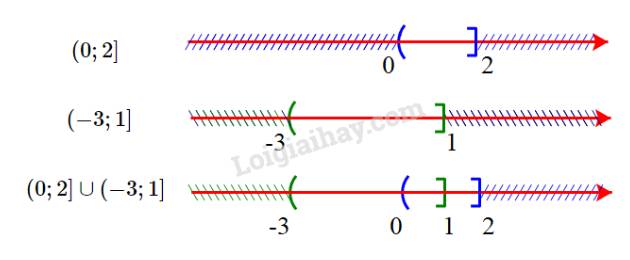
b) \((0;2] \cup (- 3;1]\)
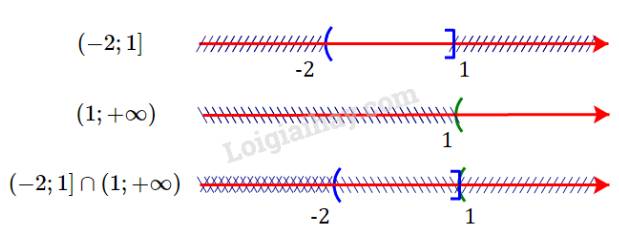
c) \(( - 2;1] \cap (1;+ \infty )\)
d) \(\mathbb{R}{\rm{\backslash }}( - \infty ;3]\)
Thảo luận (1)Hướng dẫn giảiTham khảo:
a) Ta có:
Giao của hai tập hợp là \(( - 4;1] \cap [0;3) = \left[ {0;1} \right]\)
b) Ta có:
Hợp của hai tập hợp là \((0;2] \cup ( - 3;1] = ( - 3;2]\)
c) Ta có:
Giao của hai tập hợp là \(( - 2;1] \cap (1;+ \infty )= \emptyset\)
d) Ta có:
Phần bù của tập hợp \(( - \infty ;3]\) trong \(\mathbb{R}\) là \(\mathbb{R}{\rm{\backslash }}( - \infty ;3] = (3; + \infty )\)
(Trả lời bởi Kiều Sơn Tùng)
Bài 1.16 (SGK Kết nối tri thức với cuộc sống trang 19)
Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Đọc tiếp
Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:
a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?
b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?
c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?
Thảo luận (1)Hướng dẫn giảia) Ban tổ chức đã huy động số người phiên dịch cho hội nghị đó là:
35 + 30 – 16 = 49 (người)
Vậy ban tổ chức đã huy động 49 người phiên dịch cho hội nghị đó.
b) Số người chỉ phiên dịch được tiếng Anh là:
35 – 16 = 19 (người)
Vậy có 19 người chỉ phiên dịch được tiếng Anh.
c) Số người chỉ phiên dịch được tiếng Pháp là:
30 – 16 = 14 (người)
Vậy có 14 người chỉ phiên dịch được tiếng Pháp.
(Trả lời bởi Tiếng anh123456)