Cho hình 97
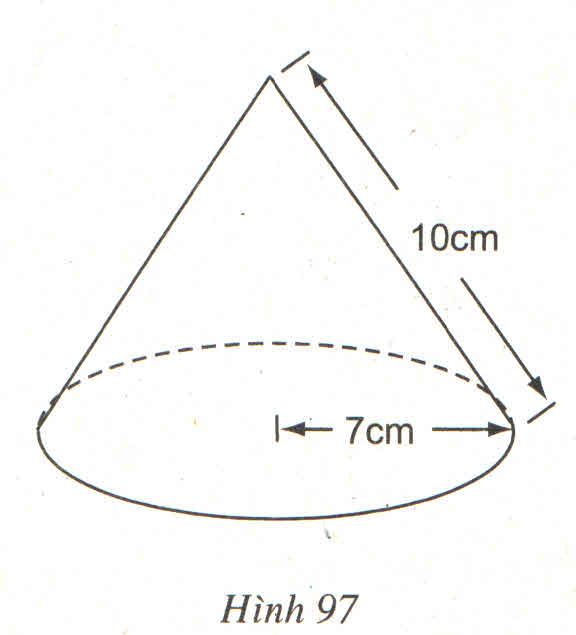
Diện tích toàn phần của hình nón là :
(A) 220 (B) 264
(C) 308 (D) 374
(Chọn \(\pi=\dfrac{22}{7}\) và tính gần đúng đến \(cm^2\) )
Cho hình 97

Diện tích toàn phần của hình nón là :
(A) 220 (B) 264
(C) 308 (D) 374
(Chọn \(\pi=\dfrac{22}{7}\) và tính gần đúng đến \(cm^2\) )
Cho hình bình hành ABCD với AB = 1, AD = x (x > 0) và \(\widehat{BAD}=60^0\)
a) Tính diện tích toàn phần S của hình tạo thành khi quay hình bình hành ABCD đúng một vòng quanh cạnh AB và diện tích toàn phần \(S_1\) của hình tạo thành khi quay quanh cạnh AD
b) Xác định giá trị x khi \(S=S_1;S=2S_1\)
Thảo luận (1)Hướng dẫn giải
Hình 98:
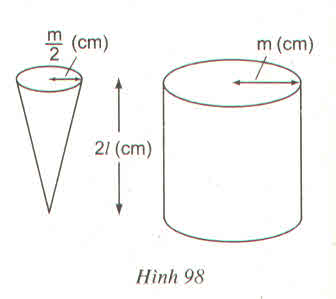
Có một hình nón, bán kính đường tròn đáy là \(\dfrac{m}{2}\left(cm\right)\), chiều cao là 2l (cm) và một hình trụ, bán kính đường tròn đáy m(cm), chiều cao 2l (cm). Người ta mức đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là :
(A) \(\dfrac{l}{6}\left(cm\right)\)
(B) \(l\left(cm\right)\)
(C) \(\dfrac{5}{6}l\left(cm\right)\)
(D) \(\dfrac{11}{6}l\left(cm\right)\)
Hãy chọn kết quả đúng ?
Thảo luận (1)Hướng dẫn giải
Nếu chiều cao và bán kính đáy của một hình nón đều tăng lên và bằng \(\dfrac{5}{4}\) so với các kích thước tương ứng ban đầu thì trong các tỉ số sau đây, tỉ số nào là tỉ số giữa thể tích của hình nón mới với thể tích của hình nón ban đầu ?
(A) \(\dfrac{5}{4}\) (B) \(\dfrac{15}{12}\)
(C) \(\dfrac{25}{16}\) (D) \(\dfrac{125}{64}\)
Thảo luận (1)Hướng dẫn giảiGọi r là bán kính đáy của hình nón, h là độ dài đường cao
Thể tích hình nón là \(\dfrac{1}{3}\pi r^2h\)
(Trả lời bởi Nguyen Thuy Hoa)
Từ một hình nón, người thợ tiện có thể tiện ra một hình trụ cao nhưng "hẹp" hoặc một hình trụ rộng nhưng "thấp"
Trong trường hợp nào thì người thợ tiện loại bỏ ít vật liệu hơn ?
Thảo luận (1)Hướng dẫn giải
Hình 99 là một hình nón :
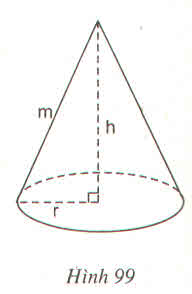
Chiều cao h (cm), bán kính đường tròn đáy là r (cm) và độ dài đường sinh m(cm) thì thể tích hình nón này là :
(A) \(\pi r^2h\left(cm^3\right)\) (B) \(\dfrac{1}{3}\pi r^2h\left(cm^3\right)\)
(C) \(\pi rm\left(cm^3\right)\) (D) \(\pi r\left(r+m\right)\left(cm^3\right)\)
Hãy chọn kết quả đúng ?
Thảo luận (2)Hướng dẫn giải
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm, người ta khoan đi một phần có dạng hình nón như hình vẽ (h.100) thì phần thể tích còn lại của nó sẽ là :
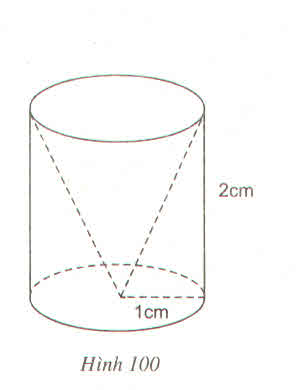
(A) \(\dfrac{2\pi}{3}\left(cm^3\right)\) (B) \(\dfrac{4\pi}{3}\left(cm^3\right)\)
(C) \(2\pi\left(cm^3\right)\) (D) \(\dfrac{8\pi}{3}\left(cm^3\right)\)
Hãy chọn kết quả đúng ?
Thảo luận (1)Hướng dẫn giải
Cho tam giác ABC vuông tại A. Gọi \(V_1,V_2,V_3\) theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC, AB và AC. Chứng minh rằng :
\(\dfrac{1}{V^2_1}=\dfrac{1}{V^2_2}+\dfrac{1}{V^2_3}\)
Thảo luận (1)Hướng dẫn giải
Hình 101 :
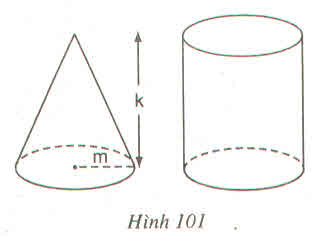
Có một hình nón, chiều cao k (cm), bán kính đường tròn đáy m(cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón. Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là :
(A) \(\dfrac{k}{4}cm\) (B) \(\dfrac{k}{3}cm\)
(C) \(\dfrac{2k}{3}cm\) (D) \(\dfrac{3k}{4}cm\)
Hãy chọn kết quả đúng ?
Thảo luận (1)Hướng dẫn giải