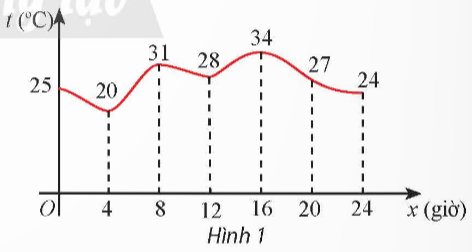
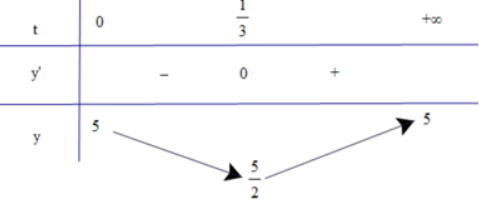
Sự phân hủy của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hòa tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t ≥ 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên).
\(y=y\left(t\right)=5-\dfrac{15t}{9t^2+1}.\)
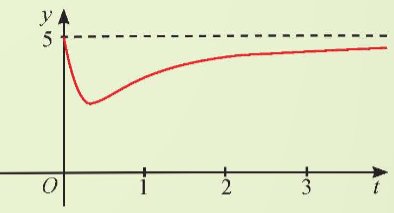
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?