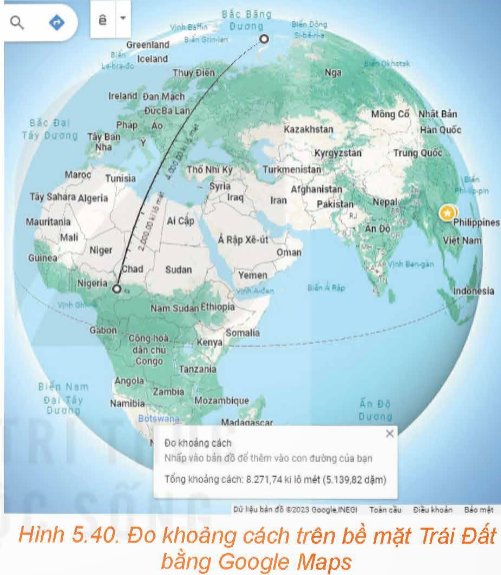
Bằng ứng dụng Google Maps, thực hiện phép đo khoảng cách trên bề mặt Trái Đất từ vị trí 10°N, 15°E đến vị trí 80°N, 70°E ta sẽ được khoảng cách 8271,74 km (H.5.40). Cơ sở toán học cho việc thiết lập phần mềm tính công thức khoảng cách trên bề mặt Trái Đất là gì?
Trong không gian Oxyz, cho mặt cầu (S) tâm I (a; b; c) bán kính R (H.5.41). Khi đó, một điểm M(x; y; z) thuộc mặt cầu (S) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện gì?
Thảo luận (1)Hướng dẫn giảiĐiểm M(x; y; z) thuộc mặt cầu (S) khi và chỉ khi IM = R
\(\Leftrightarrow\sqrt{ \left(x-a\right)^2+\left(y-b\right)^2+\left(z-c\right)^2}=R\) hay (x – a)2 + (y − b)2 + (z – c)2 = R2.
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \(\left(x+2\right)^2+y^2+\left(z+\dfrac{1}{2}\right)^2=\dfrac{9}{4}\).
a) Xác định tâm và bán kính của (S).
b) Hỏi điểm M(2; 0; 1) nằm trong, nằm ngoài hay thuộc mặt cầu (S).
Thảo luận (1)Hướng dẫn giảia) Ta viết lại phương trình mặt cầu (S) dưới dạng:
\({\left[ {x - \left( { - 2} \right)} \right]^2} + {\left( {y - 0} \right)^2} + {\left[ {z - \left( { - \frac{1}{2}} \right)} \right]^2} = {\left( {\frac{3}{2}} \right)^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( { - 2;0;\frac{{ - 1}}{2}} \right)\) và bán kính \(R = \frac{3}{2}\).
b) Ta có: \(MI = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {0 - 0} \right)}^2} + {{\left( {\frac{{ - 1}}{2} - 1} \right)}^2}} = \frac{{\sqrt {73} }}{2} > \frac{3}{2} = R\) nên điểm \(M\left( {2;0;1} \right)\) nằm ngoài mặt cầu (S).
(Trả lời bởi datcoder)
Trong không gian Oxyz, viết phương trình mặt cầu (S) trong các trường hợp sau:
a) Tâm là gốc tọa độ, bán kính R = 1.
b) Đường kính AB, với A(1; −1; 2), B(2; −3; −1).
Thảo luận (1)Hướng dẫn giảia) Mặt cầu (S) có tâm \(O\left( {0;0;0} \right)\), bán kính \(R = 1\) nên có phương trình là: \({x^2} + {y^2} + {z^2} = 1\)
b) Đoạn thẳng AB có trung điểm là \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\).
Mặt cầu (S) có bán kính \(R = \frac{1}{2}AB = \frac{1}{2}\sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( { - 3 + 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2}} = \frac{{\sqrt {14} }}{2}\) và tâm \(E\left( {\frac{3}{2}; - 2;\frac{1}{2}} \right)\). Do đó, (S): \({\left( {x - \frac{3}{2}} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{7}{2}\)
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho (S) là tập hợp các điểm M(x; y; z) có tọa độ thỏa mãn phương trình
(S): x2 + y2 + z2 – 4x + 6y – 12 = 0.
Chứng minh rằng (S) là một mặt cầu. Xác định tâm và tính bán kính của mặt cầu đó.
Thảo luận (1)Hướng dẫn giảiTa có: \({x^2} + {y^2} + {z^2} - 4x + 6y - 12 = 0\)
\( \Leftrightarrow \left( {{x^2} - 4x + 4} \right) + \left( {{y^2} + 6y + 9} \right) + {z^2} = 25\)\( \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = {5^2}\)
Do đó, (S) là mặt cầu có tâm \(I\left( {2; - 3;0} \right)\) và bán kính \(R = 5\).
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \(x^2+y^2+z^2+4x-5y+6z+\dfrac{25}{4}=0\). Xác định tâm, tính bán kính của (S).
Thảo luận (1)Hướng dẫn giảiPhương trình mặt cầu (S) đã cho tương ứng với \(a = - 2;b = \frac{5}{2};c = - 3,d = \frac{{25}}{4}\)
Nên mặt cầu (S) có tâm \(I\left( { - 2;\frac{5}{2}; - 3} \right)\), bán kính \(R = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( { - 3} \right)}^2} - \frac{{25}}{4}} = \sqrt {13} \)
(Trả lời bởi datcoder)
Tính khoảng cách trên mặt đất từ vị trí A là giao giữa kinh tuyến gốc với xích đạo đến vị trí B: 45°N, 30°E.
Thảo luận (1)Hướng dẫn giảiVì A là giao giữa kinh tuyến gốc với xích đạo nên \(A\left( {1;0;0} \right)\), do đó \(\overrightarrow {OA} \left( {1;0;0} \right)\).
Ta có: \(B\left( {\cos {{45}^o}\cos {{30}^o},\cos {{45}^o}\sin {{30}^o},\sin {{45}^o}} \right)\) nên \(\overrightarrow {OB} \left( {\frac{{\sqrt 6 }}{4};\frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{2}} \right)\), \(\overrightarrow {OA} .\overrightarrow {OB} = \frac{{\sqrt 6 }}{4}\)
Vì A, B thuộc mặt đất nên \(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = 1\)
Do đó, \(\cos \widehat {AOB} = \frac{{\overrightarrow {OA} .\overrightarrow {OB} }}{{\left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|}} = \frac{{\sqrt 6 }}{4} \Rightarrow \widehat {AOB} \approx 52,{2388^o}\)
Mặt khác, đường tròn tâm O, đi qua A, B bán kính 1 và chu vi là \(2\pi \approx 6,2832\) nên cung nhỏ AB của đường tròn có độ dài xấp xỉ bằng \(\frac{{52,2388}}{{360}}.6,2832 \approx 0,9117\)
Do 1 đơn vị độ dài trong không gian Oxyz tương ứng với 6 371km trên thực tế, nên khoảng cách giữa hai vị trí A, B xấp xỉ bằng \(0,9117.6\;371 = 5\;808,4407\left( {km} \right)\)
(Trả lời bởi datcoder)
Trên Google Maps, thực hiện phép đo khoảng cách từ vị trí 0°N, 0°E đến vị trí 45°N, 30°E và so sánh với kết quả tính được ở Luyện tập 5.
Thảo luận (1)Hướng dẫn giảiBước 1: Truy cập vào Google Maps.
Bước 2: Trên thanh tìm kiếm nhập 0°N, 0°E. Google Maps chuyển đến vị trí đó.
Bước 3. Nhấp vào vị trí đó và chuột phải chọn “Đo khoảng cách”.
Bước 4: Trên thanh tìm kiếm nhập 45°N, 30°E và nhấn enter. Google Maps đưa đến vị trí này.
Bước 5: Nhấp chuột vào vị trí này. Một đường thẳng hiện ra kèm thêm khoảng cách giữa hai vị trí này.
Kết quả như hình vẽ sau:
Từ đây ta thấy kết quả đo tương đối chính xác với kết quả tính ở luyện tập 5.
(Trả lời bởi datcoder)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình \(\left(x-\dfrac{1}{2}\right)^2+\left(y+1\right)^2+z^2=9\). Xác định tâm và bán kính của (S).
Thảo luận (1)Hướng dẫn giảiTa viết lại phương trình mặt cầu (S) dưới dạng: \({\left( {x - \frac{1}{2}} \right)^2} + {\left[ {y - \left( { - 1} \right)} \right]^2} + {\left( {z - 0} \right)^2} = {3^2}\)
Do đó, mặt cầu (S) có tâm \(I\left( {\frac{1}{2}; - 1;0} \right)\) và bán kính \(R = 3\).
(Trả lời bởi datcoder)
Trong không gian Oxyz, viết phương trình của mặt cầu (S) có tâm I(−2; 0; 5) và bán kính R = 2.
Thảo luận (1)Hướng dẫn giảiMặt cầu (S) tâm \(I\left( { - 2;0;5} \right)\), bán kính \(R = 2\) có phương trình là:
\({\left( {x + 2} \right)^2} + {y^2} + {\left( {z - 5} \right)^2} = 4\)
(Trả lời bởi datcoder)
