Thiết lập công thức tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r).
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
Hoạt động 3 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 93)
Thảo luận (1)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 93)
Biết rằng hai hình quạt tròn ứng với hai cung bằng nhau trên một đường tròn thì có diện tích bằng nhau và diện tích quạt tròn tỉ lệ với số đo của cung tương ứng với nó. Hãy thiết lập công thức tính diện tích hình quạt tròn bán kính R với cung n° bằng cách thực hiện từng bước sau:a) Tính diện tích hình quạt tròn ứng với cung 1°.b) Tính diện tích hình quạt tròn ứng với cung n°.
Đọc tiếp
Biết rằng hai hình quạt tròn ứng với hai cung bằng nhau trên một đường tròn thì có diện tích bằng nhau và diện tích quạt tròn tỉ lệ với số đo của cung tương ứng với nó. Hãy thiết lập công thức tính diện tích hình quạt tròn bán kính R với cung n° bằng cách thực hiện từng bước sau:
a) Tính diện tích hình quạt tròn ứng với cung 1°.
b) Tính diện tích hình quạt tròn ứng với cung n°.
Thảo luận (1)Hướng dẫn giảia) Đường tròn là cung có số đo bằng \(360^\circ \) và có độ dài bằng \(\pi {R^2}.\)
Suy ra diện tích hình quạt tròn ứng với cung \(1^\circ \)là: \(\frac{{\pi {R^2}}}{{360}}\)
b) Diện tích hình quạt tròn ứng với của cung \(n^\circ \) là: \(\frac{n}{{360}}.\pi {R^2}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5.9 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 94)
Cho đường tròn (O; 4 cm) và ba điểm A, B, C trên đường tròn đó sao cho tam giác ABC cân tại đỉnh A và số đo của cung nhỏ BC bằng 70°.
a) Giải thích tại sao hai cung nhỏ AB và AC bằng nhau.
b) Tính độ dài của các cung BC, AB và AC (làm tròn kết quả đến hàng phần mười).
Thảo luận (1)Hướng dẫn giải
a) Xét \(\Delta OAB\) và \(\Delta OAC\) có:
OA chung
OA = OC = R
AB = AC (do \(\Delta ABC\) cân tại A)
\(\Rightarrow \Delta OAB=\Delta OAC\) (c.c.c)
\(\Rightarrow \widehat{AOB}=\widehat{AOC}\)(hai góc tương ứng)
\(\Rightarrow \) sđ\(\overset\frown{AB}=\) sđ \(\overset\frown{AC}\)
\(\Rightarrow \overset\frown{AB}=\overset\frown{AC}\)
b) Độ dài cung BC là:
\(\frac{{70}}{{180}}.\pi .4 = \frac{{14}}{9}\pi \approx \frac{{14}}{9}.3,14 \approx 4,9 \)(cm)
Ta có: \(\widehat {AOB} + \widehat {AOC} + \widehat {BOC} = 360^\circ \)
\(\begin{array}{l} \Rightarrow 2.\widehat {AOB} + 70^\circ = 360^\circ \\ \Rightarrow 2.\widehat {AOB}\,\, = 290^\circ \\ \Rightarrow \,\,\,\,\,\,\widehat {AOB}\,\, = 145^\circ \end{array}\)
Độ dài cung AB và cung AC là: \(\frac{{145}}{{180}}.\pi .4 = \frac{{29}}{9}\pi \approx \frac{{29}}{9}.3,14 \approx 10,1 \)(cm)
(Trả lời bởi Nguyễn Quốc Đạt)
Thực hành (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 94)
Trở lại tình huống mở đầu. Hãy vẽ (tô màu) hình quạt tròn theo hướng dẫn sau:
− Vẽ đường tròn tâm O (với bán kính tùy chọn).
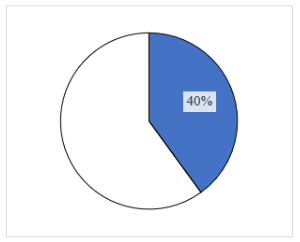
− Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 360°. Tính số đo của cung cần vẽ.
− Vẽ góc ở tâm có số đo tìm được và tô màu hình quạt tròn tương ứng.
Thảo luận (1)Hướng dẫn giải− Vẽ đường tròn tâm O (với bán kính tùy chọn).
− Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 360°.
Ta có 40% của 360° là: 360° . 40% = 144°.
− Vẽ góc ở tâm có số đo 144°: Từ bán kính làm gốc ta đo góc 144°, nối từ tâm đến điểm đạt tại 144°, ta được phần biểu đồ cần vẽ ứng với 40%.
Tô màu phần vừa biểu diễn ta được biểu đồ hình quạt tròn như sau:
(Trả lời bởi Nguyễn Quốc Đạt)
Vận dụng 2 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 94)
Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính là 5 cm, 10 cm, 15 cm, 20 cm và 30 cm (H.5.17).Giả thiết rằng người ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba), biết rằng xác xuất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
Đọc tiếp
Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính là 5 cm, 10 cm, 15 cm, 20 cm và 30 cm (H.5.17).
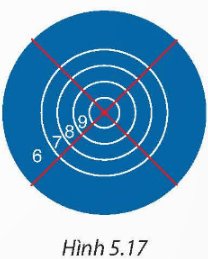
Giả thiết rằng người ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba), biết rằng xác xuất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
Thảo luận (1)Hướng dẫn giảiDiện tích của vòng 8 là: \(\pi \left( {{{15}^2} - {{10}^2}} \right) = 125\pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Diện tích hình tròn lớn nhất là: \(\pi {.30^2} = 900\pi \,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Xác suất ném trúng vòng 8 là: \(\frac{{125\pi }}{{900\pi }} = \frac{5}{{36}}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5.10 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 95)
Tính diện tích của hình quạt tròn bán kính 4 cm, ứng với cung 36°.
Thảo luận (1)Hướng dẫn giảiDiện tích của hình quạt tròn bán kính 4 cm, ứng với cung \(36^\circ \) là:
\(\frac{{{\rm{36}}}}{{{\rm{360}}}}{\rm{.\pi }}{\rm{.}}{{\rm{4}}^{\rm{2}}}{\rm{ = 1,6\pi }}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5.12 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 95)
Có hai chiếc bánh pizza hình tròn (H.5.18). Chiếc bánh thứ nhất có đường kính 16 cm được cắt thành 6 miếng đều nhau có dạng hình quạt tròn. Chiếc bánh thứ hai có đường kính 18 cm được cắt thành 8 miếng đều nhau có dạng hình quạt tròn. Hãy so sánh diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất và thứ hai.
Đọc tiếp
Có hai chiếc bánh pizza hình tròn (H.5.18). Chiếc bánh thứ nhất có đường kính 16 cm được cắt thành 6 miếng đều nhau có dạng hình quạt tròn. Chiếc bánh thứ hai có đường kính 18 cm được cắt thành 8 miếng đều nhau có dạng hình quạt tròn. Hãy so sánh diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất và thứ hai.

Thảo luận (2)Hướng dẫn giảiDiện tích bề mặt của mỗi miếng bánh cắt ra từ chiếc bánh thứ nhất là:
\(\frac{{\pi.{\left({\frac{16}{2}}\right)^2}}}{6} = \frac{{32}}{3}\pi \left( {c{m^2}} \right)\)
Diện tích bề mặt của mỗi miếng bánh cắt ra từ chiếc bánh thứ hai là:
\(\frac{{\pi.{\left({\frac{18}{2}}\right)^2}}}{8} = \frac{{81}}{8}\pi \left( {c{m^2}} \right)\)
Vì \(\frac{{32}}{3}\pi > \frac{{81}}{8}\pi \left( {c{m^2}} \right)\) nên miếng bánh cắt ra từ chiếc bánh thứ nhất lớn hơn chiếc bánh thứ hai.
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5.13 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 95)
Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 2,2 dm như hình 5.19. Tính diện tích phần giấy của chiếc quạt, biết rằng khi gấp lại, phần giấy có chiều dài khoảng 1,6 dm (làm tròn kết quả đến hàng trăm của dm2).

Thảo luận (1)Hướng dẫn giảiBán kính đường tròn nhỏ là:
\(2,2 - 1,6 = 0,6 (dm)\)
Diện tích hình vành khuyên là:
\(\pi.\left(22^2 - 0,6^2\right) = 4,48\pi (dm^2)\)
Diện tích phần giấy của chiếc quạt là:
\(4,48\pi : 2 = 2,24\pi \approx 2,24.3,14 \approx 7,03 \left( {d{m^2}} \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5.11 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 95)
Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 6 cm và 4 cm.
Thảo luận (1)Hướng dẫn giảiDiện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 6 cm và 4 cm là: \(\pi \left( {{6^2} - {4^2}} \right) = 20\pi \left( {c{m^2}} \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 2 (SGK Kết nối tri thức với cuộc sống - Tập 1 - Trang 94)
Tính diện tích của hình quạt tròn đã vẽ trong Thực hành trên nếu bán kính của nó bằng 4 cm.
Thảo luận (1)Hướng dẫn giảiHình quạt tròn ứng với cung có số đo là:
\(360^\circ .40\% = 144^\circ \)
Diện tích hình quạt tròn là:
\(S = \frac{{\rm{n}}}{{360}}.{\rm{\pi }}{{\rm{R}}^2} = \frac{{144}}{{360}}.{\rm{\pi }}{.4^2} = 6,4{\rm{\pi }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)