Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung. Hãy tìm thêm một số ví dụ khác cũng gợi nên hình ảnh đó.

Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung. Hãy tìm thêm một số ví dụ khác cũng gợi nên hình ảnh đó.

Cho mặt phẳng (α)
chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β)
(H.4.41)
Nếu (α)và (β) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?
Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
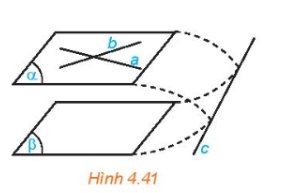
Thảo luận (1)Hướng dẫn giảiNếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
(Trả lời bởi Quoc Tran Anh Le)
Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m; n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD)
Thảo luận (1)Hướng dẫn giải
Ta có: m // BC suy ra m // (BCD).
n // BD suy ra n // (BCD).
Mặt phẳng (m,n) chứa hai đường thẳng cắt nhau m và n cùng song song với mặt phẳng (BCD) nên mặt phẳng (m, n) song song với mặt phẳng (BCD).
(Trả lời bởi Quoc Tran Anh Le)
Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43. Khi mặt bàn được đặt lên phần chân bàn thì mặt bàn luôn song song với mặt đất. Hãy giải thích tại sao.
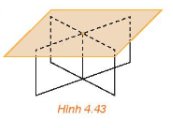
Thảo luận (1)Hướng dẫn giảiDo mặt bàn và mặt đất không có điểm chung nên chúng song song với nhau.
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Đặt một tấm bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất. Khi đó mặt bìa có trùng với mặt bàn hay không?
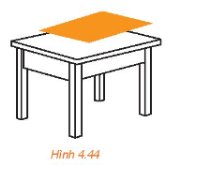
Thảo luận (1)Hướng dẫn giảiMặt bìa trùng với mặt bàn
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc các cạnh SA, SB, SC, SD sao cho
\(\dfrac{\text{MA}}{MS}=\dfrac{NB}{NS}=\dfrac{PC}{PS}=\dfrac{QD}{QS}\)=\(\dfrac{1}{2}\). Chứng minh rẳng bốn điểm M, N, P, Q đồng phẳng.
Thảo luận (2)Hướng dẫn giải
Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46)
a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).
b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?

Thảo luận (1)Hướng dẫn giảia) Vì (P) // (Q), (R) cắt (P) suy ra (R) cũng cắt (Q).
b) a và b lần lượt là giao tuyến của (R) và các mp(P), (Q) do đó a và b đồng phẳng suy ra a và b không thể chéo nhau.
Mà a và b lần lượt thuộc hai mặt phẳng song song (P) và (Q) suy ra a // b.
(Trả lời bởi Quoc Tran Anh Le)
Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).
Thảo luận (1)Hướng dẫn giảiTa có (MNPQ) // (ABCD) (chứng minh ở Ví dụ 2)
Vì vậy giao tuyến của (EMQ) với hai mặt phẳng (MNPQ) và (ABCD) song song với nhau
Trong mặt phẳng (EMQ), qua E vẽ đường thẳng ET // MQ (T thuộc CD)
Như vậy, đường thẳng ET là giao tuyến của (EMQ) và (ABCD).
(Trả lời bởi Quoc Tran Anh Le)
Cho mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ (C khác C’). Gọi D là giao điểm của AC’ và (Q) (H.4.48)
a) Các cặp đường thẳng BD và CC’, B’D và AA’ có song song với nhau không?
b) Các tỉ số\(\dfrac{AB}{BC},\dfrac{AD}{DC^,}\),ADDC′ và \(\dfrac{A^{\text{′}}B^{\text{′}}}{C\text{′}D^{\text{′}}}\) có bằng nhau không?
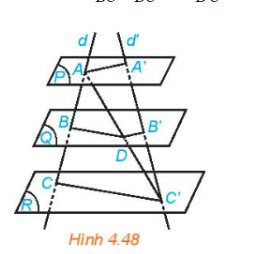
Thảo luận (1)Hướng dẫn giảia) Mặt phẳng (Q) và (R) song song với nhau, suy ra giao tuyến của (ACC') với hai mặt phẳng (Q) và (R) song song với nhau. Do đó BD // CC'
Mặt phẳng (Q) và (P) song song với nhau, suy ra giao tuyến của (C'AA') với hai mặt phẳng (Q) và (P) song song với nhau. Do đó B'D // AA'
b) Xét tam giác ACC' ta có BD // CC' suy ra \(\frac{{AD}}{{BC}} = \frac{{AD}}{{DC'}}\)
Xét tam giác C'AA' ta có B'D // AA' suy ra \(ADDC' = A'B'B'C'\)
Do đó, \(\frac{{AB}}{{BC'}} = \frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\)
(Trả lời bởi Quoc Tran Anh Le)
Trong HĐ5, cho AB = 2cm, BC = 4cm và A’B’ =3cm. Tính độ dài của đoạn thẳng B’C’.
Thảo luận (1)Hướng dẫn giảiÁp dụng định lí Thales cho ba mặt phẳng đôi một song song (P), (Q), (R) và hai cát tuyến d, d' ta có:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) suy ra \(\frac{2}{4} = \frac{3}{{B'C'}}\)
=> B'C' = 6 (cm).
(Trả lời bởi Quoc Tran Anh Le)