Cho tam giác ABC vuông tại A có AB = 2 cm, AC = 3 cm. Tính các tỉ số lượng giác của góc C.
Bài 1. Tỉ số lượng giác của góc nhọn
Bài tập 2 (SGK Cánh Diều - Tập 1 - Trang 81)
Thảo luận (1)
Bài tập 3 (SGK Cánh Diều - Tập 1 - Trang 81)
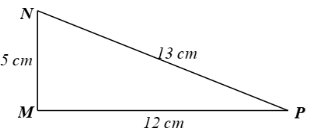
Cho tam giác MNP có MN = 5 cm, MP = 12 cm, NP = 13 cm. Chứng minh tam giác MNP vuông tại M. Từ đó, tính các tỉ số lượng giác của góc N.
Thảo luận (1)Hướng dẫn giải
Xét tam giác \(MNP\) có:
\(M{N^2} + M{P^2} = {5^2} + {12^2} = 169\).
\(N{P^2} = {13^2} = 169\).
\( \Rightarrow \Delta MNP\) vuông tại \(M\) (Định lý Pythagore đảo).
\(\sin N = \frac{{MP}}{{NP}} = \frac{{12}}{{13}}\).
\(\cos N = \frac{{MN}}{{NP}} = \frac{5}{{13}}\).
\(\tan N = \frac{{MP}}{{MN}} = \frac{{12}}{5}\).
\(\cot N = \frac{{MN}}{{MP}} = \frac{5}{{12}}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 4 (SGK Cánh Diều - Tập 1 - Trang 81)
Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63°? Vì sao?
a) sin27°; b) cos27°; c) tan27°; d) cot27°.
Thảo luận (1)Hướng dẫn giảiVì 27° và 63° là hai góc phụ nhau nên ta có:
a) sin27° = cos63°;
b) cos27° = sin63°;
c) tan27° = cot63°;
d) cot27° = tan63°.
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 5 (SGK Cánh Diều - Tập 1 - Trang 81)
Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):
a) 41°; b) 28°35’; c) 70°27’46’’.
Thảo luận (1)Hướng dẫn giảia) \(\sin 41^\circ \approx 0,66\).
\(\cos 41^\circ \approx 0,75\).
\(\tan 41^\circ \approx 0,87\).
\(\cot 41^\circ \approx 1,15\)
b) \(\sin 28^\circ 35' \approx 0,48\).
\(\cos 28^\circ 35' \approx 0,88\).
\(\tan 28^\circ 35' \approx 0,54\).
\(\cot 28^\circ 35' \approx 1,84\).
c) \(\sin 70^\circ 27'46'' \approx 0,94\).
\(\cos 70^\circ 27'46'' \approx 0,33\).
\(\tan 70^\circ 27'46'' \approx 2,82\)
\(\cot 70^\circ 27'46'' \approx 0,35\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 6 (SGK Cánh Diều - Tập 1 - Trang 81)
Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giác trị biểu thức:
A = sin 25° + cos 25° – sin 65° – cos 65°.
Thảo luận (1)Hướng dẫn giảiVì \(25^\circ \) và \(65^\circ \) là hai góc phụ nhau nên ta có: \(\sin 25^\circ = \cos 65^\circ ;\cos 25^\circ = \sin 65^\circ \).
Do đó:
\(A = \sin 25^\circ + \cos 25^\circ - \sin 65^\circ - \cos 65^\circ \\= \cos 65^\circ + \sin 65^\circ - \sin 65^\circ - \cos 65^\circ \\= 0\)
Vậy \(A = 0\)
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 7 (SGK Cánh Diều - Tập 1 - Trang 81)
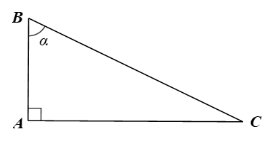
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho widehat{B}alpha.a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.b) Chứng minh: sin^2alpha+cos^2alpha1;tanalphadfrac{sinalpha}{cosalpha};cotalphadfrac{cosalpha}{sinalpha};tanalpha.cotalpha1.Từ đó, tính giá trị biểu thức: S sin2 35° + cos2 35°; T tan 61° . cot 61°.
Đọc tiếp
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho \(\widehat{B}=\alpha\).
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.
b) Chứng minh: \(\sin^2\alpha+\cos^2\alpha=1;\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha};\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha};\tan\alpha.\cot\alpha=1\).
Từ đó, tính giá trị biểu thức: S = sin2 35° + cos2 35°; T = tan 61° . cot 61°.
Thảo luận (1)Hướng dẫn giải
a) \(\sin \alpha = \frac{{AC}}{{BC}}\); \(\cos \alpha = \frac{{AB}}{{BC}}\); \(\tan \alpha = \frac{{AC}}{{AB}}\); \(\cot \alpha = \frac{{AB}}{{AC}}\).
b) Ta có:
\({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\).
\(\frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{AC}}{{BC}}:\frac{{AB}}{{BC}} = \frac{{AC}}{{BC}}.\frac{{BC}}{{AB}} = \frac{{AC}}{{AB}} = \tan \alpha \).
\(\frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{AB}}{{BC}}:\frac{{AC}}{{BC}} = \frac{{AB}}{{BC}}.\frac{{BC}}{{AC}} = \frac{{AB}}{{AC}} = \cot \alpha \).
\(\tan \alpha .\cot \alpha = \frac{{AC}}{{AB}}.\frac{{AB}}{{AC}} = 1\).
\(S = {\sin ^2}35^\circ + {\cos ^2}35^\circ = 1\).
\(T = \tan 61^\circ .\cot 61^\circ = 1\).
(Trả lời bởi Nguyễn Quốc Đạt)
Bài tập 8 (SGK Cánh Diều - Tập 1 - Trang 81)
Hình 10 mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc \(\alpha=\widehat{ABH}\). Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.
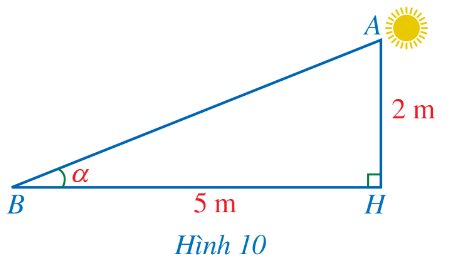
Thảo luận (1)Hướng dẫn giảiXét tam giác \(ABH\) vuông tại \(H\) có:
\(\tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{2}{5} \Rightarrow \widehat {ABH} \approx 22^\circ \).
(Trả lời bởi Nguyễn Quốc Đạt)