Cho tấm bìa có dạng hình chữ nhật AA’O’O (Hình 1a). Khi quay tấm bìa một vòng quanh OO’ cố định thì hình tạo ra giống với đồ vật quen thuộc nào?
Bài 1. Hình trụ
Khám phá 1 (SGK Chân trời sáng tạo - Tập 2 - Trang 84)
Thảo luận (1)
Thực hành 1 (SGK Chân trời sáng tạo - Tập 2 - Trang 85)
Quan sát và cho biết đường sinh, độ dài bán kính đáy và chiều cao của hình trụ trong Hình 4.
Thảo luận (1)Hướng dẫn giảiĐường sinh của hình trụ là CD.
Độ dài bán kính đáy là: 2 cm.
Chiều cao hình trụ là: 6 cm.
(Trả lời bởi datcoder)
Thực hành 2 (SGK Chân trời sáng tạo - Tập 2 - Trang 85)
Tạo lập chiếc hộp dạng hình trụ có chiều cao 10 cm, bán kính đáy 3 cm theo hướng dẫn sau:Bước 1: cắt một tấm bìa hình chữ nhật có cạnh 10 cm và cạnh 6pi cm ( approx 19 cm) (Hình 5a).Bước 2: ghép hai cạnh 10 cm của tấm bìa lại với nhau sao cho hai cạnh 6pi cm được uốn cong tạo thành hai đường tròn như Hình 5b.Bước 3: Cắt hai tấm bìa hình tròn bán kính 3 cm rồi dán vào hai đường tròn vừa tạo thành ở Bước 2, ta được chiếc hộp như yêu cầu (Hình 5c).
Đọc tiếp
Tạo lập chiếc hộp dạng hình trụ có chiều cao 10 cm, bán kính đáy 3 cm theo hướng dẫn sau:
Bước 1: cắt một tấm bìa hình chữ nhật có cạnh 10 cm và cạnh 6\(\pi \)cm (\( \approx \) 19 cm) (Hình 5a).
Bước 2: ghép hai cạnh 10 cm của tấm bìa lại với nhau sao cho hai cạnh 6\(\pi \)cm được uốn cong tạo thành hai đường tròn như Hình 5b.
Bước 3: Cắt hai tấm bìa hình tròn bán kính 3 cm rồi dán vào hai đường tròn vừa tạo thành ở Bước 2, ta được chiếc hộp như yêu cầu (Hình 5c).
Thảo luận (1)Hướng dẫn giảiLấy giấy làm thủ công tương tự các bước như ở trên.
(Trả lời bởi datcoder)
Khám phá 2 (SGK Chân trời sáng tạo - Tập 2 - Trang 85)
Hình khai triển của một hình trụ có bán kính đáy r, chiều cao h (Hình 6a) gồm hai hình tròn và một hình chữ nhật (Hình 6b). Diện tích của hình chữ nhật trong Hình 6b được gọi là diện tích xung quanh của hình trụ
Hãy tính diện tích xung quanh của hình trụ theo r và h.
Thảo luận (1)Hướng dẫn giảiDiện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
(Trả lời bởi datcoder)
Vận dụng (SGK Chân trời sáng tạo - Tập 2 - Trang 86)
Một nhà máy dự định sản xuất thùng phuy đựng dầu nhớt dạng hình trụ có đường kính đáy 0,6 m và chiều cao 0,9 m (Hình 7). Bỏ qua diện tích các mép thùng, hãy tính diện tích thép cần để sản xuất 100 thùng phuy như vậy (kết quả làm tròn đến hàng phần trăm).
Thảo luận (1)Hướng dẫn giảiDiện tích thép xung quanh cần để sản xuất 1 thùng phuy là:
\({S_{xq}} = 2\pi rh = \pi dh\) = \(\pi \).0,6.0,9 = 0,54\(\pi \) (m2)
Diện tích toàn phần của 1 thùng phi là:
\({S_{tp}} = {S_{xq}} + {S_{day}} = 0,54\pi + 2.{\left( {\frac{{0,6}}{2}} \right)^2}.\pi = 0,72\pi \) (m2)
Diện tích thép cần để sản xuất 100 thùng phuy là:
S = 100. 0,72\(\pi \) = 226,19 (m2)
Vậy diện tích thép cần để sản xuất 100 thùng phuy là 226,19 m2.
(Trả lời bởi datcoder)
Khám phá 3 (SGK Chân trời sáng tạo - Tập 2 - Trang 86)
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và...
Đọc tiếp
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.
a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.
b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và h.
Thảo luận (1)Hướng dẫn giảia) Thể tích V của lượng nước trong bình A là: V = S.h
Thể tích V của lượng nước trong bình B là: V = S.h
b) Thể tích V của lượng nước trong bình B là: V = S.h = \(\pi \)r2h.
(Trả lời bởi datcoder)
Thực hành 3 (SGK Chân trời sáng tạo - Tập 2 - Trang 87)
Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng \(\frac{2}{3}\)chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Thảo luận (1)Hướng dẫn giảiThể tích của bể là: V = \(\pi \)r2h = \(\pi \).1,52.2,1 = 4,725\(\pi \) (m3).
Thể tích lượng nước trong bể là:
\(V' = \frac{2}{3}V = \frac{2}{3}.4,725\pi \) = 10 (m3).
(Trả lời bởi datcoder)
Bài tập 1 (SGK Chân trời sáng tạo - Tập 2 - Trang 87)
Trong các hình sau đây, hình nào là hình trụ?
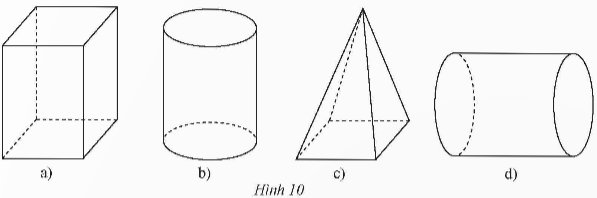
Thảo luận (1)Hướng dẫn giảiHình b và Hình d là hình trụ.
(Trả lời bởi datcoder)
Bài tập 2 (SGK Chân trời sáng tạo - Tập 2 - Trang 87)
Tìm chiều cao, bán kính đáy và diện tích xung quanh, thể tích của mỗi hình trụ sau:
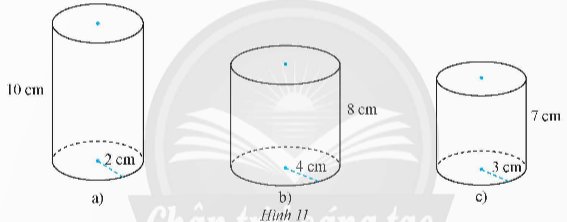
Thảo luận (1)Hướng dẫn giảia) - Chiều cao: 10 cm.
- Bán kính đáy: 2 cm.
- Diện tích xung quanh là: \({S_{xq}} = 2\pi rh\) = 2\(\pi \).2.10 = 125,66 (cm2).
- Thể tích hình trụ là: V = S.h = \(\pi \)r2h =\(\pi \).22.10 = 125,66 (cm3).
b) - Chiều cao: 8 cm.
- Bán kính đáy: 4 cm.
- Diện tích xung quanh là: \({S_{xq}} = 2\pi rh\) = 2\(\pi \).4.8 = 201, 06 (cm2).
- Thể tích hình trụ là: V = \(\pi \)r2h = \(\pi \).42.8 = 402, 12 (cm3).
c) - Chiều cao: 7 cm.
- Bán kính đáy: 3 cm.
- Diện tích xung quanh là: \({S_{xq}} = 2\pi rh\) = 2\(\pi \).3.7 = 131, 95 (cm2).
- Thể tích hình trụ là: V =\(\pi \)r2h =\(\pi \).32.7 = 197,92 (cm3).
(Trả lời bởi datcoder)
Bài tập 3 (SGK Chân trời sáng tạo - Tập 2 - Trang 87)
Tạo lập hình trụ có bán kính đáy 4 cm, chiều cao 7 cm.
Thảo luận (1)Hướng dẫn giải- Bước 1: Cắt một tấm bìa hình chữ nhật có cạnh 7 cm và cạnh 8\(\pi \)cm (\( \approx \) 25 cm).
- Bước 2: Ghép hai cạnh 7 cm của tấm bìa lại với nhau sao cho hai cạnh 8\(\pi \)cm được uốn cong tạo thành hai đường tròn.
- Bước 3: Cắt hai tấm bìa hình tròn bán kính 4 cm rồi dán vào hai đường tròn vừa tạo thành ở Bước 2, ta được chiếc hộp như yêu cầu.
(Trả lời bởi datcoder)