Bài 1. Hàm số và đồ thị của hàm số y = ax² (a ≠ 0)

Hướng dẫn giải

a) Thay R = 10 vào \(S = \pi {R^2}\), ta có: \(S = \pi {10^2} = 100\pi \) (cm²).

b) Diện tích S phải là hàm số của biến số R.

(Trả lời bởi datcoder)

Hướng dẫn giải

a) Hàm số y = 0,75x² có hệ số là 0,75

Hàm số y = - 3x² có hệ số là – 3

Hàm số \(y = \frac{1}{4}{x^2}\) có hệ số là \(\frac{1}{4}\)

b) Với x = - 2; x = 2 ta thay lần lượt vào y = 0,75x² ta được y = 3; y = 3.

Với x = - 2; x = 2 ta thay lần lượt vào y = - 3x²  ta được y = -12; y = -12.

Với x = - 2; x = 2 ta thay lần lượt vào \(y = \frac{1}{4}{x^2}\) ta được y = 1; y = 1.

(Trả lời bởi datcoder)

Hướng dẫn giải

a) Công thức tính diện tích S (cm²) của viên gạch đó là S = x² .

b) Thay x = 20 ta được S = 20² = 400 cm² .

Thay x = 30 ta được S = 30² = 900 cm² .

Thay x = 60 ta được S = 60² = 3600 cm² .

(Trả lời bởi datcoder)

Hướng dẫn giải

(Trả lời bởi datcoder)

Hướng dẫn giải

- Khi x=−4: y=1/4⋅(−4)^2=4 và y=−1/4⋅(−4)^2=−4.

- Khi x=−2: y=1/4⋅(−2)^2=1 và y=−1/4⋅(−2)^2=−1.

- Khi x=0: y=0 cho cả hai hàm.

- Khi x=2: y=1/4⋅(2)^2=1 và y=−1/4⋅(2)^2=−1.

- Khi x=4: y=1/4⋅(4)^2=4 và y=−1/4⋅(4)^2=−4

x | y=1/4x^2 | y=−1/4x^2 |

|---------|-------------------------|-----------------------------|

| -4 | 4 | -4 |

| -2 | 1 | -1 |

| 0 | 0 | 0 |

| 2 | 1 | -1 |

| 4 | 4 | -4 |

 

(Trả lời bởi hocthemmoingay.)

Hướng dẫn giải

a) Sau 2 giây quãng đường vật di chuyển được là:

s = 5.2² = 20 (m)

Sau 2 giây vật này cách mặt đất số mét là:

125 - s = 125 - 20 = 105 (m)

Sau 3 giây quãng đường vật di chuyển được là:

s = 5.3² = 45 (m)

Sau 3 giây vật này cách mặt đất số mét là:

125 - s = 125 - 45 = 80 (m)

b) Để vật này tiếp đất thì s = 125 thay vào 5t² = 125

Do đó: t = 5 giây (vì t > 0)

Vậy sau 5 giây thì vật tiếp đất.

(Trả lời bởi datcoder)

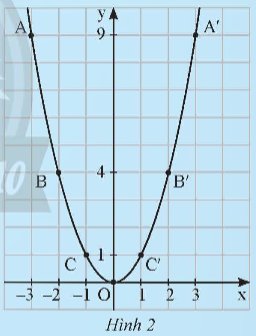
Hướng dẫn giải

a) Đồ thị của hàm số có vị trí phía trên so với trục hoành.

b) Các cặp điểm A và A’, B và B’, C và C’ đối xứng với nhau qua trục tung.

c) Điểm thấp nhất của đồ thị là điểm O(0;0).

(Trả lời bởi datcoder)

Hướng dẫn giải

a)

Lấy các điểm A(-2;6), B(-1; \( - \frac{3}{2}\)), O(0;0), B’(1; \( - \frac{3}{2}\)), A’(2;-6).

Đồ thị hàm số \(y =  - \frac{3}{2}{x^2}\) là một đường cong đi qua các điểm nêu trên và có dạng như hình dưới.

Nhận xét: Đồ thị nằm bên dưới trục hoành.

(Trả lời bởi datcoder)

Hướng dẫn giải

Ta có bảng giá trị:

Trên mặt phẳng tọa độ, lấy các điểm A(−2; 8), B(−1; 2), O(0; 0), B'(1; 2), A'(2; 8).

Đồ thị hàm số y = 2x² là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.

(Trả lời bởi datcoder)

Hướng dẫn giải

a) Với v = 3 m/s ta có \(K = \frac{1}{2}{.3^2} = \frac{9}{2}\) J

Với v = 4 m/s ta có \(K = \frac{1}{2}{.4^2} = 8\)J

b) Với K = 32 J ta có: \(32 = \frac{1}{2}{v^2}\)

suy ra v² = 64. Do đó, v = 8 (m/s).

(Trả lời bởi datcoder)