Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
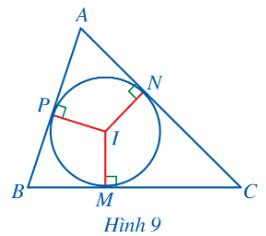
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).

Trong Hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?
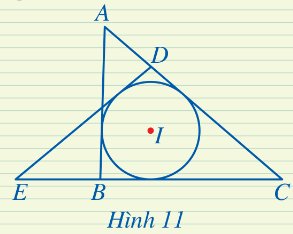
Thảo luận (1)Hướng dẫn giảiĐường tròn (I) là đường tròn nội tiếp tam giác ABC vì nó tiếp xúc với ba cạnh AB, BC, CA.
Đường tròn (I) là đường tròn nội tiếp tam giác CDE vì nó tiếp xúc với ba cạnh DE, DC, EC.
(Trả lời bởi datcoder)
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC (hình 7). Đường tròn (O; OB) có phải là đường tròn ngoại tiếp tam giác ABC hay không?
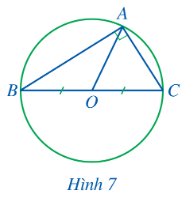
Thảo luận (1)Hướng dẫn giảiVì O là trung điểm của BC nên AO là đường trung tuyến của tam giác ABC.
Xét tam giác ABC vuông tại A có AO là đường trung tuyến ứng với cạnh huyền BC nên ta có: \(OA = OB = OC = \frac{{BC}}{2}\)
Vậy 3 điểm A, B, C thuộc đường tròn đường kính OB nên (O; OB) là đường tròn ngoại tiếp tam giác ABC.
(Trả lời bởi datcoder)
Cho tam giác đều ABC nội tiếp đường tròn (O; 2cm). Tính AB.
Thảo luận (1)Hướng dẫn giải
Chứng minh
Kẻ đường trung trực AH của tam giác ABC suy ra \(O \in AH,\widehat {OHB} = 90^\circ .\)
Vì tam giác đều ABC nội tiếp đường tròn (O; 2cm) nên OA = OB = 2cm.
Ta lại có: AH là đường trung trực của tam giác đều ABC nên AH đồng thời là đường trung tuyến, do đó \(OH = \frac{1}{2}AO = \frac{1}{2}.2 = 1cm,AH = 3OH = 3.1 = 3cm.\)
Xét tam giác OHB vuông tại H, áp dụng định lý Pytago ta có: \(BH = \sqrt {B{O^2} - O{H^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 cm.\)
Xét tam giác AHB vuông tại H, áp dụng định lý Pytago ta có:
\(AB = \sqrt {{3^2} + {{\sqrt 3 }^2}} = 2\sqrt 3 cm.\)
Vậy\(AB = 2\sqrt 3 cm.\)
(Trả lời bởi datcoder)
Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó.
Thảo luận (1)Hướng dẫn giảiCách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó:
Bước 1. Lấy một điểm M bất kì trên đường tròn.
Bước 2. Đặt đỉnh vuông của ê ke trùng với điểm M.
Bước 3. Kẻ hai đường thẳng đi qua hai cạnh góc vuông của ê kê, hai đường thẳng này cắt đường tròn lần lượt tại hai điểm A, B (khác điểm M).
Bước 4. Nối đoạn thẳng AB, khi đó AB là đường kính của đường tròn.
Bước 5. Lấy O là trung điểm của AB, khi đó O là tâm của đường tròn đã cho.
Thật vậy, ∆MAB vuông tại M nên đường tròn ngoại tiếp tam giác MAB có tâm là trung điểm O của cạnh huyền AB.
(Trả lời bởi datcoder)
Cho tam giác ABC có O là giao điểm của ba đường trung trực (Hình 5).
a) Các đoạn thẳng OA, OB, OC có bằng nhau không?
b) Đặt R = OA. Đường tròn (O;R) có phải là đường tròn ngoại tiếp tam giác ABC hay không? Vì sao?
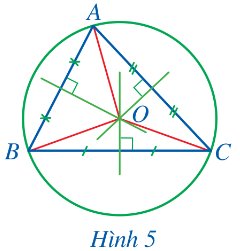
Thảo luận (1)Hướng dẫn giảia) Vì O là giao điểm của ba đường trung trực của tam giác ABC nên điểm O cách đều ba đỉnh của tam giác ABC.
Do đó OA = OB = OC.
b) Ta có OA = OB = OC = R nên ba điểm A, B, C cùng nằm trên đường tròn (O; R) hay đường tròn (O; R) đi qua ba đỉnh của tam giác.
Vậy đường tròn (O; R) là đường tròn ngoại tiếp tam giác ABC.
(Trả lời bởi datcoder)
Cho biết các đỉnh của tam giác ABC (Hình 2) có thuộc đường tròn (O) hay không.
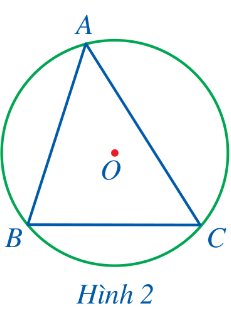
Thảo luận (1)Hướng dẫn giảiCác đỉnh A, B, C của tam giác ABC đều thuộc đường tròn (O).
(Trả lời bởi datcoder)
Trong thiết kế logo ở Hình 1, đường tròn đi qua ba đỉnh của tam giác.

Đường tròn đi qua ba đỉnh của tam giác được gọi là gì?
Thảo luận (1)Hướng dẫn giảiĐường tròn đi qua ba đỉnh của tam giác được gọi là đường tròn ngoại tiếp tam giác đó.
(Trả lời bởi datcoder)
Quan sát Hình 4 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tam giác ABC, đường tròn nào ngoại tiếp tam giác ABD?
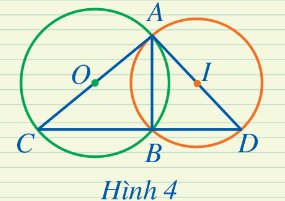
Thảo luận (1)Hướng dẫn giải⦁ Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC vì nó đi qua ba đỉnh A, B, C của tam giác ABC.
⦁ Đường tròn (I) là đường tròn ngoại tiếp tam giác ABD vì nó đi qua ba đỉnh A, B, D của tam giác ABD.
(Trả lời bởi datcoder)
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).
a) AM, BN, CP có là các đường trung trực của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?
c) Tính AM theo a.
d) Tính OA theo a.
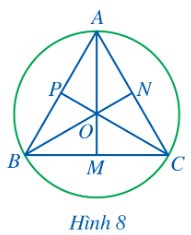
Thảo luận (1)Hướng dẫn giảia) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là ba đường trung trực của tam giác ABC. Do đó AM, BN, CP lần lượt là trung trực của BC, AC, AB.
b) Do ba đường trung trực của tam giác ABC cắt nhau tại O nên O cách đều 3 đỉnh A, B, C (tính chất 3 đường trung trực của tam giác).
Vậy O là tâm đường tròn ngoại tiếp tam giác ABC.
c) Xét tam giác đều ABC cạnh a có trung tuyến AM nên \(BM = \frac{1}{2}BC = \frac{a}{2}.\)
AM là đường trung trực của tam giác ABC (cmt) nên \(AM \bot BC\) do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác ABM vuông tại M có:
\(A{M^2} = A{B^2} - B{M^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\) (Pytago)
\(AM = \frac{{\sqrt 3 a}}{2}.\)
d) Ta có: AM là trung tuyến của tam giác ABC, O là trọng tâm nên \(OA = \frac{2}{3}AM = \frac{2}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{3}.\)
(Trả lời bởi datcoder)