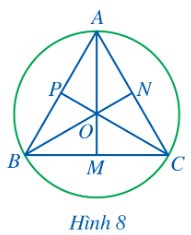
a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là ba đường trung trực của tam giác ABC. Do đó AM, BN, CP lần lượt là trung trực của BC, AC, AB.
b) Do ba đường trung trực của tam giác ABC cắt nhau tại O nên O cách đều 3 đỉnh A, B, C (tính chất 3 đường trung trực của tam giác).
Vậy O là tâm đường tròn ngoại tiếp tam giác ABC.
c) Xét tam giác đều ABC cạnh a có trung tuyến AM nên \(BM = \frac{1}{2}BC = \frac{a}{2}.\)
AM là đường trung trực của tam giác ABC (cmt) nên \(AM \bot BC\) do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác ABM vuông tại M có:
\(A{M^2} = A{B^2} - B{M^2} = {a^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\) (Pytago)
\(AM = \frac{{\sqrt 3 a}}{2}.\)
d) Ta có: AM là trung tuyến của tam giác ABC, O là trọng tâm nên \(OA = \frac{2}{3}AM = \frac{2}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{3}.\)