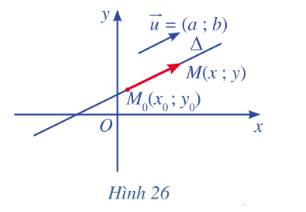
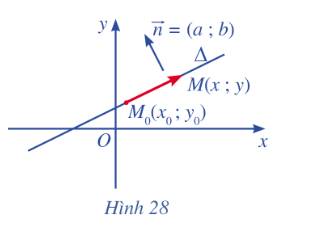
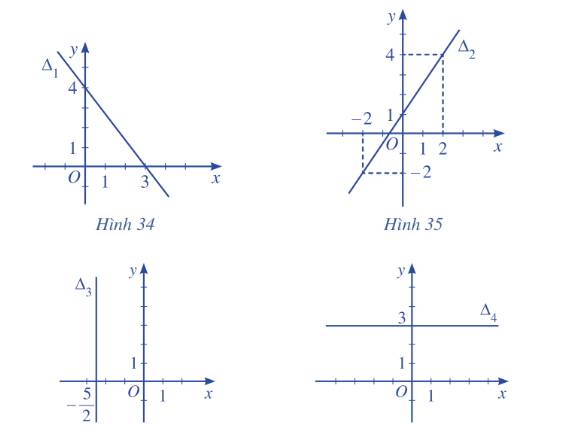
Một máy bay cất cánh từ sân bay theo một đường thẳng nghiêng với phương nằm ngang một góc 20°, vận tốc cất cánh là 200 km/h. Hình 24 minh họa hình ảnh đường bay của máy bay trên ra màn hình ra đa của bộ phận không lưu. Để xác định vị trí của máy bay tại những thời điểm quan trọng (chẳng hạn: 30 s, 60 s, 90 s, 120 s), người ta phải lập phương trình đường thẳng mô tả đường bay.

Làm thế nào để lập phương trình đường thẳng trong mặt phẳng tọa độ?