Bài 5d: Bài tập ôn luyện
Các câu hỏi tương tự
Cho hs y= x^4 - 2x^2 +2 . Diện tích S của tam giác có 3 đỉnh là 3 điểm cực trị của đồ thị hàm số đã cho có giá trị là?
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
f(x)dfrac{1}{2}x^4-3x^2+dfrac{3}{2}
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình f’’(x) 0
c) Biện luận theo tham số m số nghiệm của phương trình: x^4 – 6x^2 + 3 m
Đọc tiếp
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
\( f(x)=\dfrac{1}{2}x^4-3x^2+\dfrac{3}{2}\)
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là nghiệm của phương trình \(f’’(x) = 0\)
c) Biện luận theo tham số \(m\) số nghiệm của phương trình: \(x^4 – 6x^2 + 3 = m\)
tìm khoảng đồng biến và nghịch biến của hàm số y = g(x) = f(2x-4)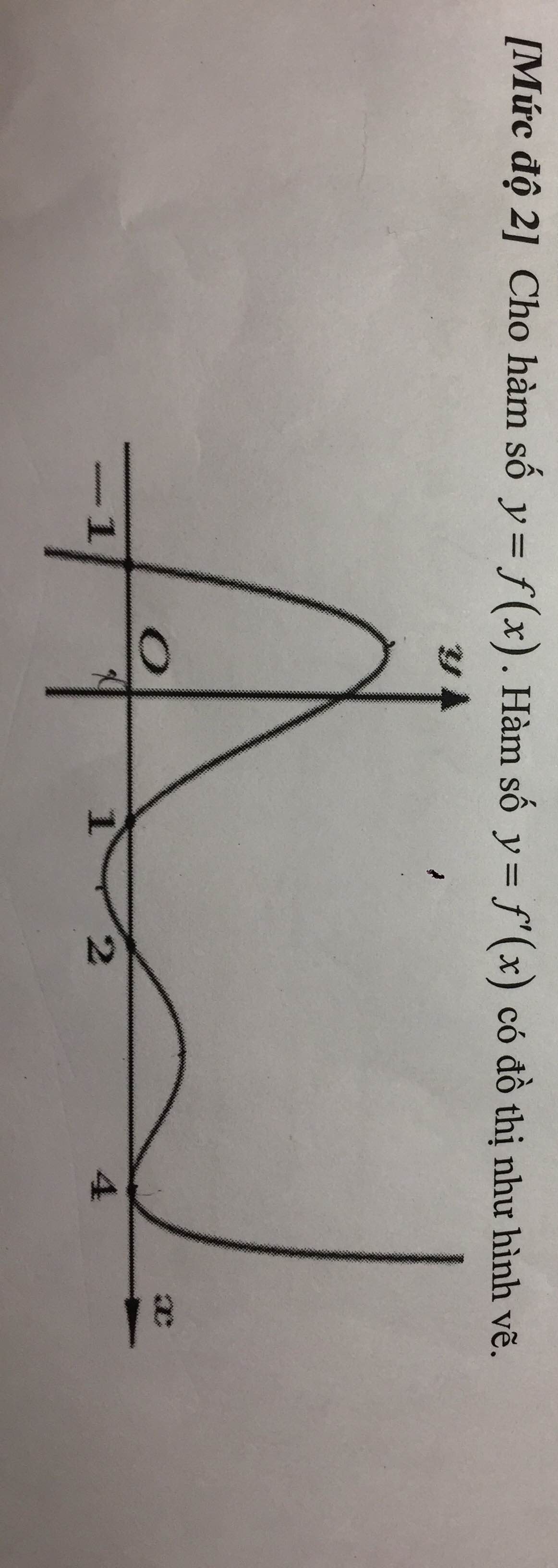
Nêu cách tìm cực đại, cực tiểu của hàm số nhờ đạo hàm. Tìm các cực trị của hàm số \(y = x^4 – 2x^2 + 2\)
Cho hàm số: \(f(x)=\dfrac{1}{3}x^3−\dfrac{1}{2}x^2−4x+6\)
a) Giải phương trình \(f’(\sin x) = 0\)
b) Giải phương trình \(f’’(\cos x) = 0\)
c) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình \(f’’(x) = 0\)
Số điểm cực đại của hàm số \(y=x^4+100\) là:
0 1 2 3Cho hàm số:
y -x^4 + 2mx^2 – 2m + 1 ( m là tham số) có đồ thị (C_m)
a) Biện luận theo m số cực trị của hàm số
b) Với giá trị nào của m thì (C_m) cắt trục hoành?
c) Xác định m
để (C_m) có cực đại, cực tiểu
Đọc tiếp
Cho hàm số:
\(y = -x^4 + 2mx^2 – 2m + 1\) ( \(m\) là tham số) có đồ thị \((C_m)\)
a) Biện luận theo \(m\) số cực trị của hàm số
b) Với giá trị nào của \(m\) thì \((C_m)\) cắt trục hoành?
c) Xác định \(m
\) để \((C_m)\) có cực đại, cực tiểu
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số
f(x) -x^3+3x^2+9x+2
b) Giải bất phương trình f’(x-1)0
c) Vẽ phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x_0, biết rằng f’’(x_0) -6
Đọc tiếp
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số \((C)\) của hàm số
\(f(x) = -x^3+3x^2+9x+2\)
b) Giải bất phương trình \(f’(x-1)>0\)
c) Vẽ phương trình tiếp tuyến của đồ thị \((C)\) tại điểm có hoành độ \(x_0\), biết rằng \(f’’(x_0) = -6\)
Tiệm cận ngang của đồ thị hàm số y = 3x +1/x-1 là:






