vẽ hình chứng minh nha!!
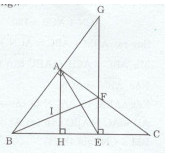
Cho tam giác ABC vuông tại A (AB < AC) . Trên cạnh BC lấy điểm E sao cho BE = BA . Kẽ đường thẳng qua E vuông góc với BC cắt AC ở F và cắt AB ở G
a/ Chứng minh tam giác AEF cân
b/ Chứng minh : AC = GE
c/ Kẻ AH vuông góc BC tại H . Gọi I là giao điểm của AH và BF . Chứng minh tam giác AIF cân
a) Xét 2 \(\Delta\) vuông \(ABF\) và \(EBF\) có:
\(\widehat{BAF}=\widehat{BEF}=90^0\left(gt\right)\)
\(AB=EB\left(gt\right)\)
Cạnh BF chung
=> \(\Delta ABF=\Delta EBF\) (cạnh huyền - cạnh góc vuông).
=> \(AF=EF\) (2 cạnh tương ứng).
=> \(\Delta AEF\) cân tại \(F.\)
b) Xét 2 \(\Delta\) vuông \(ABC\) và \(EBG\) có:
\(\widehat{BAC}=\widehat{BEG}=90^0\left(gt\right)\)
\(AB=EB\left(gt\right)\)
\(\widehat{ABC}\) chung
=> \(\Delta ABC=\Delta EBG\) (cạnh góc vuông - góc nhọn kề).
=> \(AC=GE\) (2 cạnh tương ứng).
c) Theo câu a) ta có \(\Delta ABF=\Delta EBF.\)
=> \(\widehat{AFB}=\widehat{EFB}\) (2 góc tương ứng).
Hay \(\widehat{AFI}=\widehat{EFB}\) (1).
+ Vì:
\(\left\{{}\begin{matrix}AH\perp BC\left(gt\right)\\EF\perp BC\left(gt\right)\end{matrix}\right.\)
=> \(AH\) // \(EF\) (từ vuông góc đến song song).
Hay \(AI\) // \(EF.\)
=> \(\widehat{AIF}=\widehat{EFB}\) (vì 2 góc so le trong) (2).
Từ (1) và (2) => \(\widehat{AFI}=\widehat{AIF}.\)
=> \(\Delta AIF\) cân tại \(A\left(đpcm\right).\)
Chúc bạn học tốt!











