Chương IV - Hàm số y = ax^2 (a khác 0). Phương trình bậc hai một ẩn
Các câu hỏi tương tự
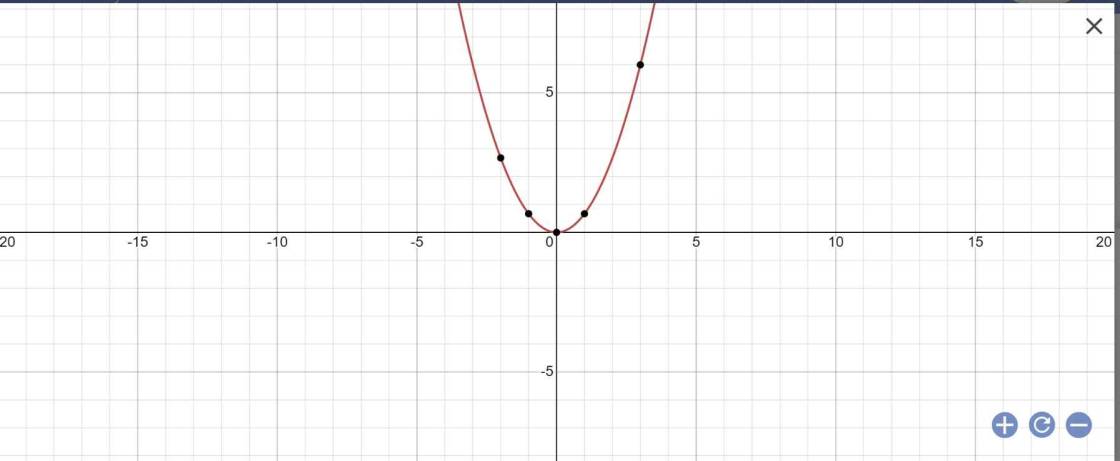
Vẽ hai đô thị hàm số y=\(\dfrac{1}{4}x^2\) và y=2x+3. Sau đó tìm tọa độ giao điểm của chúng?
.
.
.
.
.
.
.
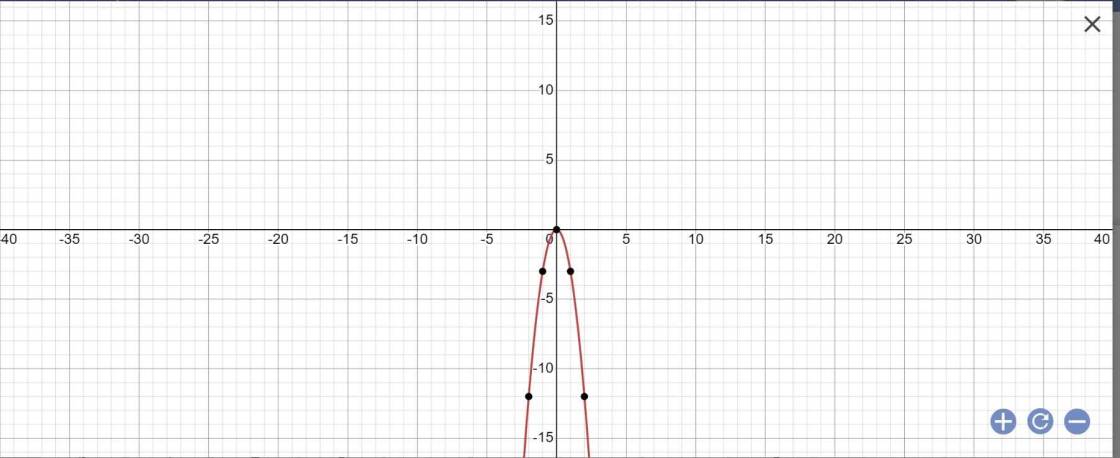
Cho hàm số y = -\(\dfrac{3}{2}\)x\(^2\) có đồ thị (P) và y = -2x + \(\dfrac{1}{2}\) có đồ thị (d)
1/ Vẽ (P) và (d) trên cùng một hệ trục tọa độ vuông góc. Xác định tọa độ các giao điểm của (P) và (d).
2/ Tìm tọa độ những điểm trên (P) thỏa tính chât tổng hoành độ và tung độ của điểm đó bằng -4.
Cho 3 số dương x,y,z
chứng minh \(\sqrt{\dfrac{x}{y+2}}+\sqrt{\dfrac{y}{x+2}}+\sqrt{\dfrac{z}{x+y}}>2\)
cho x,y là hai số thực dương thỏa mản x3+y3=xy-\(\dfrac{1}{27}\)
tính giá trị của biểu thức p=\(\left(x+y+\dfrac{1}{3}\right)^3-\dfrac{3}{2}\left(x+y\right)+2021\)
Bài 2 giải hệ pt : \(\left\{{}\begin{matrix}\dfrac{2}{|x-1|}-5\left(y-1\right)=-3\\\dfrac{1}{\left|x-1\right|}-2\left(1-y\right)=3\end{matrix}\right.\)
mọi người cho em hỏi bài này cái ????
đề : cho 3 số thực x,y,z thoả mãn đk x+y+z=0 và xyz khác 0
tính gt bt P = \(\dfrac{x^2^{ }}{y^2+z^2-x^2}+\dfrac{y^2}{z^2+x^2-y^2}+\dfrac{z^2}{x^2+y^2-z^2}\)
Bài 1: Cho hàm số f(x) = ax5 + bx3 + cx có giá trị nguyên với mọi x nguyên và f(1), f(2), f(3) đạt giá trị lớn nhất khi a, b, c dương. Tìm a,b,c
Bài 2: Nếu x, y ∈ Z thỏa mãn 3x2 + x = 3y2 + y thì x - y; 2x + 2y + 1; 3x + 3y + 1 là các số chính phương
Dạ nhờ mọi người giúp dùm em bài này, em cảm ơn ạ
Vẽ đồ thị các hàm số sau ( cho x:-2:-1;0;1;2)
1) y=x^2
2) y=-x^2
3) y=2x^2
4) y=-2x^2
5) y=3x^2 phần 2
Xem chi tiết
Giải giúp mình vài hệ pt này nha
thanks nhiều
1.left{{}begin{matrix}sqrt{x^2+x+y+1}+x+sqrt{y^2+x+y+1}+y15sqrt{x^2+x+y+1}-x+sqrt{y^2+x+y+1}-y2end{matrix}right.
2.left{{}begin{matrix}left(1-dfrac{12}{y+3x}right)sqrt{x}2left(1+dfrac{12}{y+3x}right)sqrt{y}6end{matrix}right.
3.left{{}begin{matrix}x^3+y^38x+y+2xy2end{matrix}right.
4.left{{}begin{matrix}x^3+12yy^3+12xend{matrix}right.
5.left{{}begin{matrix}x^3-3xy^3-3yx^6+y^61end{matrix}right.
6.left{{}begin{matrix}x^2-2xy+3y^292x^2-13xy+15y^2...
Đọc tiếp
Giải giúp mình vài hệ pt này nha
thanks nhiều
1.\(\left\{{}\begin{matrix}\sqrt{x^2+x+y+1}+x+\sqrt{y^2+x+y+1}+y=15\\\sqrt{x^2+x+y+1}-x+\sqrt{y^2+x+y+1}-y=2\end{matrix}\right.\)
2.\(\left\{{}\begin{matrix}\left(1-\dfrac{12}{y+3x}\right)\sqrt{x}=2\\\left(1+\dfrac{12}{y+3x}\right)\sqrt{y}=6\end{matrix}\right.\)
3.\(\left\{{}\begin{matrix}x^3+y^3=8\\x+y+2xy=2\end{matrix}\right.\)
4.\(\left\{{}\begin{matrix}x^3+1=2y\\y^3+1=2x\end{matrix}\right.\)
5.\(\left\{{}\begin{matrix}x^3-3x=y^3-3y\\x^6+y^6=1\end{matrix}\right.\)
6.\(\left\{{}\begin{matrix}x^2-2xy+3y^2=9\\2x^2-13xy+15y^2=0\end{matrix}\right.\)