Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
Cho tam giác ABC vuông có AB = 9cm , AC = 12cm . Vẽ phân giác BD
a) Tính BD , AD
b) Qua D vẽ đường thẳng vuông góc với BC tại H , cắt tia BA tại E . chứng minh \(\Delta ABC\) đồng dạng \(\Delta HDC\) . Tính diện tích \(\Delta ADE\)
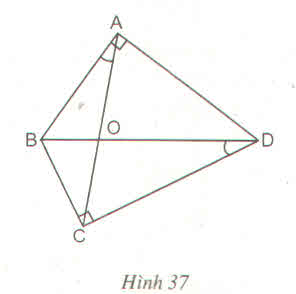
Bài 1. Cho tứ giác ABCD có 2 góc vuông tại đỉnh A và C, hai đường chéo AC và BC cắt nhau tại O
góc BAO và góc BDC
a. tam giác ABO đồng dạng tam giác DCO
b. tam giác BCO đồng dạng ADO
Bài 2. Tứ giác ABCD có 2 đg chéo AC và BD cắt nhau tại O, góc ABD=góc ACD. Gọi E là giao điểm 2 đg thẳng AD và BC
câu a và b như trên
c. EA.ED=EB.EC
Cho ΔABC vuông tại A (AB<AC), đường cao AH (H∈BC), BD là phân giác góc ABC (DϵAC), BD cắt AH tại M.
a) Chứng minh ΔABH ∼ΔCBA; ΔBAM∼ΔBCD.
b) Chứng minh \(\frac{AB}{AD}=\frac{CB}{CD}\)và AB.AM= BC.HM. TRường hợp có BC = 3AB, chứng minh SABC = 36.SBHM.
Cho hình chữ nhật ABCD có AB = 8cm , BC = 6cm , vẽ AH vuông góc với đường chéo BD ( H\(\in\) BD)
a) Tính độ dài dường cao AH
b) Chứng \(\Delta AHB\) \(\sim\) \(\Delta BCD\)
c) Chứng minh AD2 = DH . DB
Cho hình thang ABCD (AB//CD) biết AB=2,5cm ; AD=3,5cm ; BD=5cm và \(\widehat{DAB}=\widehat{DBC}\)
a, C/m: ΔABD\(\sim\)ΔBDC
b, Tính BC, DC
c, Gọi E là giao điểm của AC và BD. Qua E kẻ đường thẳng bất kì cắt AB, CD lần lượt tại M và N. Tính \(\frac{ME}{NE}\)
Cho tam giác MnQ nhọn; MN MQ. Hai đường cao NK và QE cắt nhau tại H.a)Cm: Delta MNKsimDelta MQE. Từ đó suy ra: MN.MEMK.MQb)Cm: HQ.HEHN.HKc)Cm: widehat{MNQ}widehat{MKE}d)Cm: MHperpNQe)Cm: IM là tia phân giác widehat{KIE} với I là giao điểm MH và NQ
Đọc tiếp
Cho tam giác MnQ nhọn; MN < MQ. Hai đường cao NK và QE cắt nhau tại H.
a)Cm: \(\Delta MNK\)\(\sim\)\(\Delta MQE\). Từ đó suy ra: MN.ME=MK.MQ
b)Cm: HQ.HE=HN.HK
c)Cm: \(\widehat{MNQ}\)=\(\widehat{MKE}\)
d)Cm: MH\(\perp\)NQ
e)Cm: IM là tia phân giác \(\widehat{KIE}\) với I là giao điểm MH và NQ
Bài 1 :
Cho ΔABC nhọn (ABAC) và hai đường cao BD và CE.
a) Chứng minh : ΔADB đồng dạng với ΔAEC
b) Chứng minh : AD.BC AB.DE
c) Tia ED cắt BC tại O. Chứng minh : OD.OE OB.OC
Bài 2 :
Cho ΔABC vuông tại A (ABAC) có AH là đường cao (H ∈ BC)
a) Chứng minh : ΔHBA đồng dạng với ΔABC và HB.AC HA.AB
b) Chứng minh : HA2 HB.HC
c) Gọi M là trung điểm của AH. Trên tia đối của tia AC lấy điểm N sao cho ANdfrac{1}{2}AC. Chứng minh : ΔBHM đồng dạng với ΔBAN.
d) Chứng minh góc BMN 90o
Đọc tiếp
Bài 1 :
Cho ΔABC nhọn (AB>AC) và hai đường cao BD và CE.
a) Chứng minh : ΔADB đồng dạng với ΔAEC
b) Chứng minh : AD.BC = AB.DE
c) Tia ED cắt BC tại O. Chứng minh : OD.OE = OB.OC
Bài 2 :
Cho ΔABC vuông tại A (AB<AC) có AH là đường cao (H ∈ BC)
a) Chứng minh : ΔHBA đồng dạng với ΔABC và HB.AC = HA.AB
b) Chứng minh : HA2 = HB.HC
c) Gọi M là trung điểm của AH. Trên tia đối của tia AC lấy điểm N sao cho \(AN=\dfrac{1}{2}AC\). Chứng minh : ΔBHM đồng dạng với ΔBAN.
d) Chứng minh góc BMN = 90o
cho DeltaABC.các đường cao BD và CE cắt nhau tại H
a)chứng minh:DeltaABD~DeltaACE
b)chứng minh:BE.BABH.BD
c)chứng minh:widehat{ADE}widehat{ABC}
d)kẻ DFperpBC,gọi M và N là trung điểm của BF và DF.chứng minh:CNperpDM
MIK CẦN PHẦN d NHA
Đọc tiếp
cho \(\Delta\)ABC.các đường cao BD và CE cắt nhau tại H
a)chứng minh:\(\Delta\)ABD~\(\Delta\)ACE
b)chứng minh:BE.BA=BH.BD
c)chứng minh:\(\widehat{ADE}=\widehat{ABC}\)
d)kẻ DF\(\perp\)BC,gọi M và N là trung điểm của BF và DF.chứng minh:CN\(\perp\)DM
MIK CẦN PHẦN d NHA
Cho tam giác ABC có ba góc nhọn , hai đường cao BE và CF cắt nhau tại H ( E in AC , F in AB )
a) Chứng minh Delta AEBsimDelta AFC
b) Chứng minh Delta AEFsimDelta ABC
c) Cho EB EC , M là trung điểm EC . Đường thẳng vuông góc với BM tại I vẽ từ E cắt đường thẳng vuông góc với EC vẽ từ C tại N. Chứng minh S_{CMIN} frac{4}{5} S_{CEN}
Đọc tiếp
Cho tam giác ABC có ba góc nhọn , hai đường cao BE và CF cắt nhau tại H ( E \(\in\) AC , F \(\in\) AB )
a) Chứng minh \(\Delta AEB\sim\Delta AFC\)
b) Chứng minh \(\Delta AEF\sim\Delta ABC\)
c) Cho EB = EC , M là trung điểm EC . Đường thẳng vuông góc với BM tại I vẽ từ E cắt đường thẳng vuông góc với EC vẽ từ C tại N. Chứng minh S\(_{CMIN}\) = \(\frac{4}{5}\) S\(_{CEN}\)