Ôn tập: Tam giác đồng dạng
Các câu hỏi tương tự
Cho hình thang ABCD (AB//CD) biết AB=2,5cm ; AD=3,5cm ; BD=5cm và \(\widehat{DAB}=\widehat{DBC}\)
a, C/m: ΔABD\(\sim\)ΔBDC
b, Tính BC, DC
c, Gọi E là giao điểm của AC và BD. Qua E kẻ đường thẳng bất kì cắt AB, CD lần lượt tại M và N. Tính \(\frac{ME}{NE}\)
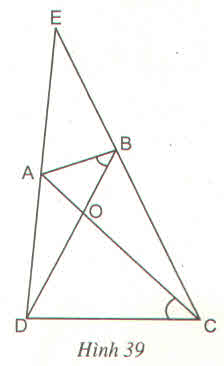
Cho tứ giác ABCD có 2 đường chéo AC và BD cắt nhau tại O; ABD =ACD. Gọi E là giao điểm của 2 cạnh kéo dài AD và BC. Cmr :
a) Tam giác AOB đồng dạng DOC
b) tam giác AOD đồng dạng tam giác BOC
c) EA. ED =EB. EC
Cho tam giác ABC vuông có AB = 9cm , AC = 12cm . Vẽ phân giác BD
a) Tính BD , AD
b) Qua D vẽ đường thẳng vuông góc với BC tại H , cắt tia BA tại E . chứng minh \(\Delta ABC\) đồng dạng \(\Delta HDC\) . Tính diện tích \(\Delta ADE\)
cho DeltaABC.các đường cao BD và CE cắt nhau tại H
a)chứng minh:DeltaABD~DeltaACE
b)chứng minh:BE.BABH.BD
c)chứng minh:widehat{ADE}widehat{ABC}
d)kẻ DFperpBC,gọi M và N là trung điểm của BF và DF.chứng minh:CNperpDM
MIK CẦN PHẦN d NHA
Đọc tiếp
cho \(\Delta\)ABC.các đường cao BD và CE cắt nhau tại H
a)chứng minh:\(\Delta\)ABD~\(\Delta\)ACE
b)chứng minh:BE.BA=BH.BD
c)chứng minh:\(\widehat{ADE}=\widehat{ABC}\)
d)kẻ DF\(\perp\)BC,gọi M và N là trung điểm của BF và DF.chứng minh:CN\(\perp\)DM
MIK CẦN PHẦN d NHA
Bài 1. Cho tứ giác ABCD có 2 góc vuông tại đỉnh A và C, hai đường chéo AC và BC cắt nhau tại O
góc BAO và góc BDC
a. tam giác ABO đồng dạng tam giác DCO
b. tam giác BCO đồng dạng ADO
Bài 2. Tứ giác ABCD có 2 đg chéo AC và BD cắt nhau tại O, góc ABD=góc ACD. Gọi E là giao điểm 2 đg thẳng AD và BC
câu a và b như trên
c. EA.ED=EB.EC
Cho Delta ABC có H là trực tâm . Gọi P là 1 điểm thuộc đoạn thẳng AB , gọi Q là 1 điểm thuộc đoạn thẳng AC sao cho widehat{BHP}widehat{CHQ}90^0 . Gọi M là trung điểm của đoạn thẳng BC. Chứng minh rằng HM vuông góc với PQ .P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn ạ!
Đọc tiếp
Cho \(\Delta ABC\) có H là trực tâm . Gọi P là 1 điểm thuộc đoạn thẳng AB , gọi Q là 1 điểm thuộc đoạn thẳng AC sao cho \(\widehat{BHP}=\widehat{CHQ}=90^0\) . Gọi M là trung điểm của đoạn thẳng BC. Chứng minh rằng HM vuông góc với PQ .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ em với ạ, em cám ơn ạ!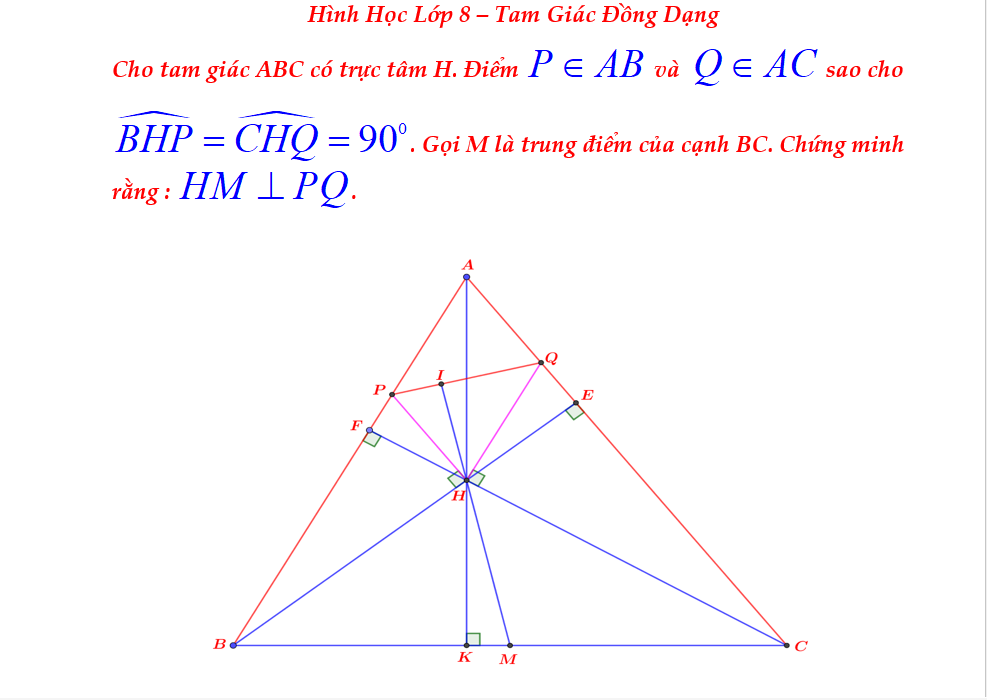
Cho hình thoi ABCD có widehat{ABC} 90^0. Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho widehat{MON}widehat{DAC}. Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!Em cám ơn nhiều lắm ạ!
Đọc tiếp
Cho hình thoi ABCD có \(\widehat{ABC}< 90^0\). Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho \(\widehat{MON}=\widehat{DAC}\). Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Bài 1 :
Cho ΔABC nhọn (ABAC) và hai đường cao BD và CE.
a) Chứng minh : ΔADB đồng dạng với ΔAEC
b) Chứng minh : AD.BC AB.DE
c) Tia ED cắt BC tại O. Chứng minh : OD.OE OB.OC
Bài 2 :
Cho ΔABC vuông tại A (ABAC) có AH là đường cao (H ∈ BC)
a) Chứng minh : ΔHBA đồng dạng với ΔABC và HB.AC HA.AB
b) Chứng minh : HA2 HB.HC
c) Gọi M là trung điểm của AH. Trên tia đối của tia AC lấy điểm N sao cho ANdfrac{1}{2}AC. Chứng minh : ΔBHM đồng dạng với ΔBAN.
d) Chứng minh góc BMN 90o
Đọc tiếp
Bài 1 :
Cho ΔABC nhọn (AB>AC) và hai đường cao BD và CE.
a) Chứng minh : ΔADB đồng dạng với ΔAEC
b) Chứng minh : AD.BC = AB.DE
c) Tia ED cắt BC tại O. Chứng minh : OD.OE = OB.OC
Bài 2 :
Cho ΔABC vuông tại A (AB<AC) có AH là đường cao (H ∈ BC)
a) Chứng minh : ΔHBA đồng dạng với ΔABC và HB.AC = HA.AB
b) Chứng minh : HA2 = HB.HC
c) Gọi M là trung điểm của AH. Trên tia đối của tia AC lấy điểm N sao cho \(AN=\dfrac{1}{2}AC\). Chứng minh : ΔBHM đồng dạng với ΔBAN.
d) Chứng minh góc BMN = 90o
Cho ΔABC vuông tại A (AB<AC), đường cao AH (H∈BC), BD là phân giác góc ABC (DϵAC), BD cắt AH tại M.
a) Chứng minh ΔABH ∼ΔCBA; ΔBAM∼ΔBCD.
b) Chứng minh \(\frac{AB}{AD}=\frac{CB}{CD}\)và AB.AM= BC.HM. TRường hợp có BC = 3AB, chứng minh SABC = 36.SBHM.