c là hàm số của t vì với mỗi giá trị của t thì có 1 và chỉ 1 giá trị của c.
$1. Hàm số và đồ thị
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong bài toán ở phần mở đầu, ta đã biết công thức tính quãng đường đi được \(S\left( m \right)\) của vật rơi tự do theo thời gian \(t\left( s \right)\) là: \(S = \frac{1}{2}g{t^2}\), trong đó \(g\) là gia tốc rơi tự do, \(g \approx 9,8\left( {m/{s^2}} \right)\).
a) Với mỗi giá trị \(t = 1,t = 2\), tính giá trị tương ứng của S.
b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của S?
Để xây dựng phương án kinh doanh cho một loại sản phẩm, doanh nghiệp tính toán lợi nhuận y (đồng) theo công thức sau: \(y = - 200{x^2} + 92{\rm{ }}000x - 8{\rm{ }}400{\rm{ }}000\), trong đó x là số sản phẩm loại đó được bán ra.
a) Với mỗi giá trị x = 100, x = 200, tính giá trị tương ứng của y.
b) Với mỗi giá trị của x có bao nhiêu giá trị tương ứng của y?
Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có không lượng đến 250g như trong bảng sau:a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x(g) hay không? Nếu đúng, hãy xác định những công thức tính y.b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g.
Đọc tiếp
Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có không lượng đến 250g như trong bảng sau:
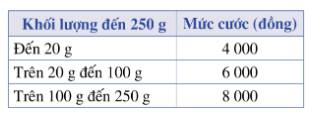
a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x(g) hay không? Nếu đúng, hãy xác định những công thức tính y.
b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g.
Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá.Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe.Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất?
Đọc tiếp
Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá.
Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe.
Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất?
Galileo Galilei (1564 - 1642). sinh tại thành phố Pisa (Italia). là nhà bác học vī đại của thời kì Phục Hưng. Ông được mệnh danh là “cha đẻ của khoa học hiện đại”. Trước Galileo. người ta tin rằng vật nặng rơi nhanh hơn vật nhẹ, ông đã bác bỏ điểu này bằng thí nghiệm nổi tiếng ở tháp nghiêng Pisa. Từ thí nghiệm của Galileo, các nhà khoa học sau này được truyển cảm hứng rằng chúng ta chỉ có thể rút ra tri thúc khoa học từ các quy luật khách quan của tự nhiên, chứ không phải từ niềm tin.Làm thế nà...
Đọc tiếp
Galileo Galilei (1564 - 1642). sinh tại thành phố Pisa (Italia). là nhà bác học vī đại của thời kì Phục Hưng. Ông được mệnh danh là “cha đẻ của khoa học hiện đại”. Trước Galileo. người ta tin rằng vật nặng rơi nhanh hơn vật nhẹ, ông đã bác bỏ điểu này bằng thí nghiệm nổi tiếng ở tháp nghiêng Pisa. Từ thí nghiệm của Galileo, các nhà khoa học sau này được truyển cảm hứng rằng chúng ta chỉ có thể rút ra tri thúc khoa học từ các quy luật khách quan của tự nhiên, chứ không phải từ niềm tin.
Làm thế nào để mô tả được mối liên hệ giữa thời gian t và quãng đuờmg đi đuợc S của vật rơi tự do? Làm thế nào để có được hình ảnh hình học mình hoạ mối liên hệ giữa hai đại lượng đó?
Cho đồ thị hàm số y fleft( x right) như Hình 8.a) Trong các điểm có tọa độ left( {1; - 2} right),left( {0;0} right),left( {2; - 1} right), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?b) Xác định fleft( 0 right);fleft( 3 right).c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
Đọc tiếp
Cho đồ thị hàm số \(y = f\left( x \right)\) như Hình 8.
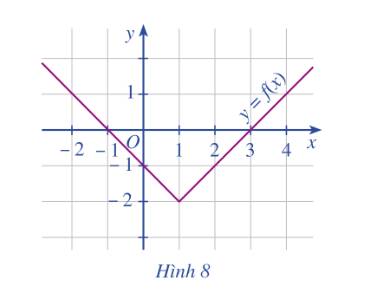
a) Trong các điểm có tọa độ \(\left( {1; - 2} \right),\left( {0;0} \right),\left( {2; - 1} \right)\), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right);f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
Cho hàm số \(y = - 2{x^2}\).
a) Điểm nào trong các điểm có tọa độ \(\left( { - 1; - 2} \right),\left( {0;0} \right),\left( {0;1} \right),\left( {2021;1} \right)\) thuộc đồ thị của hàm số trên?
b) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng \( - 2;3\) và 10.
c) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng \( - 18\).
Xét hàm số \(y = f\left( x \right) = {x^2}\)
a) Tính các giá trị \({y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)\) tương ứng với giá trị \({x_1} = - 1;{x_2} = 1\).
b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\).
Cho hai hàm số \(y = 2x + 1\left( 1 \right)\) và \(y = \sqrt {x - 2} \left( 2 \right)\)
a) Nêu biểu thức xác định mỗi hàm số trên.
b) Tìm x sao cho mỗi biểu thức trên có nghĩa.


