Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.
Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi qua đỉnh và trung điểm của cạnh đối diện (tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp (ba đường trung tuyến) có cùng đi qua một điểm không?
Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33)
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức:
BG = ? BN, CG = ? CP;
BG = ? GN, CG = ? GP.
Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A,B,C rồi vẽ tam giác ABC. (H.9.29)
Vẽ hai đường trung tuyến BN, CP, chúng cát nhau tại G, tia AG cắt cạnh BC tại M.
- AM có phải là đường trung tuyến của tam giác ABC không?
- Hãy xác định các tỉ số \(\dfrac{{GA}}{{MA}};\dfrac{{GB}}{{NB}};\dfrac{{GC}}{{PC}}\)
Cho góc xOy khác góc bẹt. Dùng compa dựng đường tròn tâm O cắt Ox tại A và cắt Oy tại B. Sau đó dựng hai đường tròn tâm A, tâm B có bán kính bằng nhau sao cho chúng cắt nhau tại M nằm nên trong góc xOy. Chứng minh rằng tia OM là tia phân giác của góc xOy.
Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Cho tam giác ABC có hai đường phân giác AM, BN cắt nhau tại điểm I. Hỏi CI có là đường phân giác của góc C không?
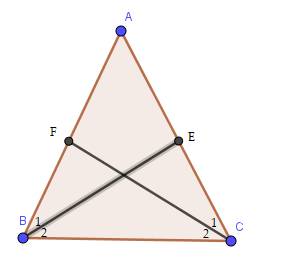
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
