Question

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \(x^2+y^2-6x-6y+14=0\)

Tìm điểm M thuộc trục hoành sao cho từ M kẻ được hai tiếp tuyến của (C) mà góc giữa hai tiếp tuyến đó bằng \(60^0\)

Answer 1

Đường tròn (C) có tâm I (3 ; 3) và có bán kính

\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)

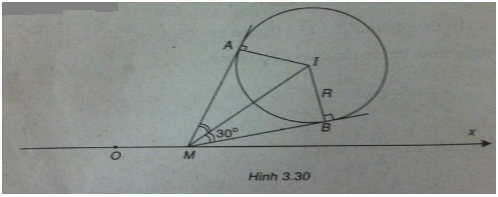
Điểm M(x;0) thuộc Ox.

Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:

\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)

\(\Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)

\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)

\(\Leftrightarrow {x^2} - 6x + 2 = 0\)

\(\Leftrightarrow x = 3 \pm \sqrt 7\)

Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :

\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\)