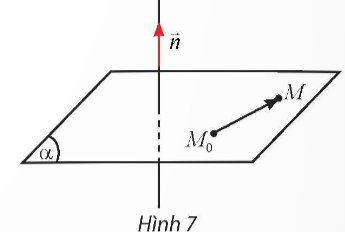
Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M0(x0; y0; z0) và nhận \(\overrightarrow{n}=\left(A;B;C\right)\) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian.
a) Tìm tọa độ của \(\overrightarrow{M_0M}\).
b) Tính tích vô hướng của \(\overrightarrow{n}.\overrightarrow{M_0M}\).
c) Lập phương trình tổng quát của mặt phẳng (α).
a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right) = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
b) Ta có: \(\vec n.\overrightarrow {{M_0}M} = A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right)\)
c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M} = 0\).
Suy ra \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
Vậy phương trình mặt phẳng \(\left( \alpha \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)


