Question

Trong không gian Oxyz, cho mặt phẳng (α) đi qua điểm M₀(1; 2; 3) và nhận \(\overrightarrow{n}\) = (7; 5; 2) làm vectơ pháp tuyến. Gọi M(x; y; z) là một điểm tùy ý trong không gian. Tính tích vô hướng \(\overrightarrow{n}.\overrightarrow{M_0M}\) theo x, y, z.

Answer 1

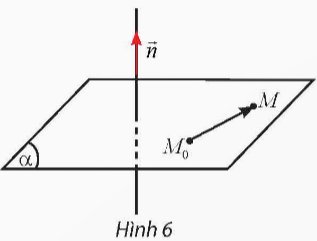
Toạ độ của vectơ \(\overrightarrow {{M_0}M} \) là \(\left( {x - 1;y - 2;z - 3} \right)\)

Suy ra \(\vec n.\overrightarrow {{M_0}M}  = 7\left( {x - 1} \right) + 5\left( {y - 2} \right) + 2\left( {z - 3} \right) = 7x + 5y + 2z - 23\)