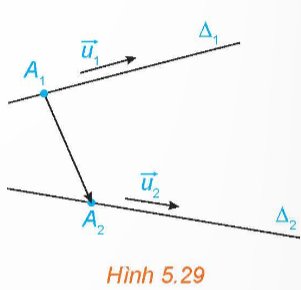
Trong không gian $O x y z$, cho hai đường thẳng $\mathrm{D}_1 ; \mathrm{D}_2$ lần lượt đi qua các điểm $\mathrm{A}_1\left(\mathrm{x}_1 ; \mathrm{y}_1 ; \mathrm{z}_1\right), \mathrm{A}_2\left(\mathrm{x}_2 ; \mathrm{y}_2 ; \mathrm{z}_2\right)$ và tương ứng có vectơ chỉ phương $\overrightarrow{u_1}=\left(a_1 ; b_1 ; c_1\right), \overrightarrow{u_2}=\left(a_2 ; b_2 ; c_2\right)$ (H.5.29).
a) Tim điều kiện đối với $\overrightarrow{u_1}$ và $\overrightarrow{u_2}$ để $\mathrm{D}_1$ và $\mathrm{D}_2$ song song hoặc trùng nhau.
b) Giả sử $\left[\overrightarrow{u_1}, \overrightarrow{u_2}\right] \neq \overrightarrow{0}$ và $\overrightarrow{A_1 A_2} \cdot\left[\overrightarrow{u_1}, \overrightarrow{u_2}\right]=0$ thì $\mathrm{D}_1$ và $\mathrm{D}_2$ có cắt nhau hay không?
c) Giả sử $\overrightarrow{A_1 A_2} \cdot\left[\overrightarrow{u_1}, \overrightarrow{u_2}\right] \neq 0$ thì $\mathrm{D}_1$ và $\mathrm{D}_2$ có chéo nhau hay không?
