Question

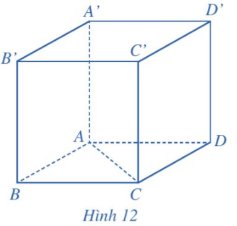
Trong không gian, cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh bằng 3 cm (Hình 12). 

a) Tính góc giữa hai vectơ \(\overrightarrow{AC},\overrightarrow{A'D'}.\)

b) Tính \(\left|\overrightarrow{AC}\right|.\left|\overrightarrow{A'D'}\right|.\cos\left(\overrightarrow{AC},\overrightarrow{A'D'}\right).\)

Answer 1

Ta có A’D’//AD.

Góc giữa \(\overrightarrow {AC} \;\)và\(\;\overrightarrow {A'D'} \)= \(\;\overrightarrow {AC} \) và \(\overrightarrow {AD} \).

a) Mà ABCD là hình vuông => \(\widehat {CAD} = 45^\circ \)

b) \(\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A'D'|} \) = AC.AD = 3.3 = 9.

cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \))= cos(\(\overrightarrow {AC} ,\overrightarrow {AD} )\)= \(\frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1\).