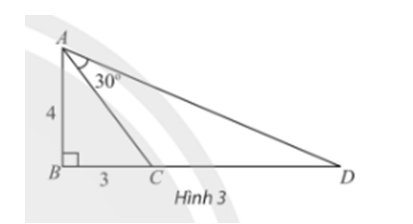
Xét tam giác ABC vuông tại B có:
\(\tan \widehat {BAC} = \frac{3}{4}\)
Suy ra, \(\tan \widehat {BAD} = \tan \left( {\widehat {BAC} + \widehat {CAD}} \right) = \tan \left( {\widehat {BAC} + {{30}^0}} \right)\)
\( = \frac{{\tan \widehat {BAC} + \tan {{30}^0}}}{{1 - \tan \widehat {BAC}.\tan {{30}^0}}} = \frac{{\frac{3}{4} + \frac{{\sqrt 3 }}{3}}}{{1 - \frac{3}{4}.\frac{{\sqrt 3 }}{3}}} \approx 2,34\)
Xét tam giác vuông ABD vuông tại B có:
\(\begin{array}{l}BD = AB.\tan \widehat {BAD} = 4.2,34 \approx 9,36\\ \Rightarrow CD = BD - BC \approx 9,36 - 3 \approx 6,36\end{array}\)