Khẳng định đúng là a, khẳng định sai là b.
- Khẳng định a đúng vì
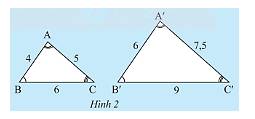
Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
- Khẳng định b sai vì
Nếu\(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) thì tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi \(k \ne 1\) thì \(AB \ne A'B'AC \ne A'C'BC \ne B'C'\) nên hai tam giác không bằng nhau.