Ta tiến hành đo và nhận thấy hình \({\beta _1}\) là hình đồng dạng phối cành với hình \(\beta \) theo tỉ số \(k > 1\).
Ta tiến hành đo và nhận thấy hình \({\beta _4}\) là hình đồng dạng phối cành với hình \(\beta \) theo tỉ số \(k < 1\).
Cho hai hình đồng dạng phối cảnh \(H\) và \({H_1}\), biết tỉ số đồng dạng \(k = \frac{2}{3}\).
a) Tính \(x,y\).
b) So sánh hình \({H_1}\) và hình \(H'\).
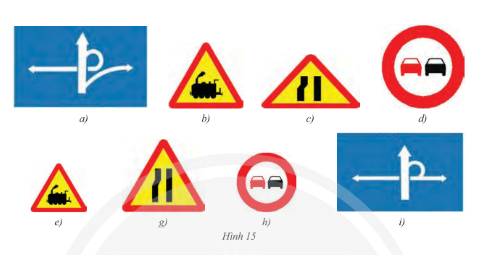
Trong các hình dưới đây, hai hình nào đồng dạng với nhau?
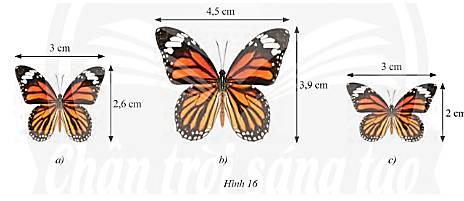
Trong Hình 9b, c, d, Hình nào đồng dạng với Hình 9a. Giải thích.
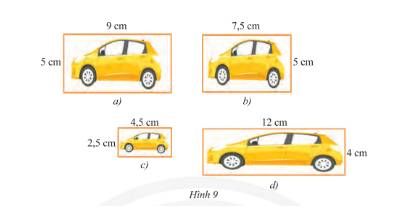
Trong các Hình 17b, c, d hình nào đồng dạng với Hình 17a? Giải thích?
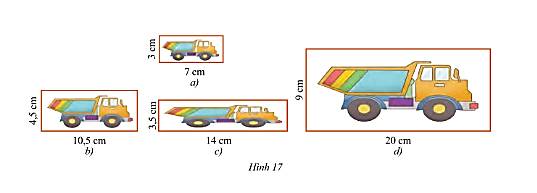
Trong Hình 8 dưới đây, hãy chọn ra các cặp hình đồng dạng với nhau.
a) Cho đoạn thẳng \(AB\) và điểm \(O\). Kẻ các tia \(OA,OB\). Trên tia \(OA,OB\) lần lượt lấy các điểm \(A',B'\) sao cho \(OA' = 3OA,OB' = 3OB\) (Hình 1a).
i) \(A'B'\) có song song với \(AB\) không.
ii) Tính tỉ số \(\frac{{A'B'}}{{AB}}\).
b) Cho tam giác \(ABC\) và điểm \(O\). Kẻ các tia \(OA,OB,OC\). Trên tia \(OA,OB,OC\) lần lượt lấy các điểm \(A',B',C'\) sao cho \(OA' = 3OA,OB' = 3OB,OC' = 3OC\) (Hình 1b).
i) Tính và so sánh các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\).
ii) Chứng minh tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\).
Trong các hình dưới đây, hãy chỉ ra các cặp hình đồng dạng.
Hình 18b là Hình 18a sau khi phóng to với \(k = 1,5\). Nếu kích thức của Hình 18a là \(4 \times 6\)thì kích thước của Hình 18b là bao nhiêu?
Tương tự, thực hiện cách dựng như trên với tứ giác \(ABCD\). Trên tia \(OA,OB,OC,OD\) lần lượt lấy các điểm \(A',B',C',D'\) sao cho \(OA' = 2OA,OB' = 2OB,OC' = 2OC,OD' = 2OD\) (Hình 2).
Tính và so sánh các tỉ số \(\frac{{A'B'}}{{AB}};\frac{{A'D'}}{{AD}};\frac{{B'C'}}{{BC}};\frac{{C'D'}}{{CD}}\).
