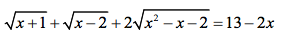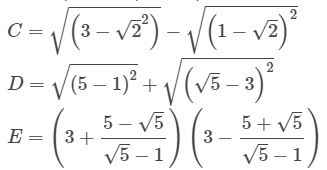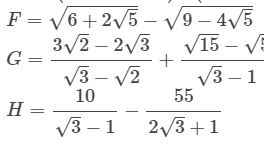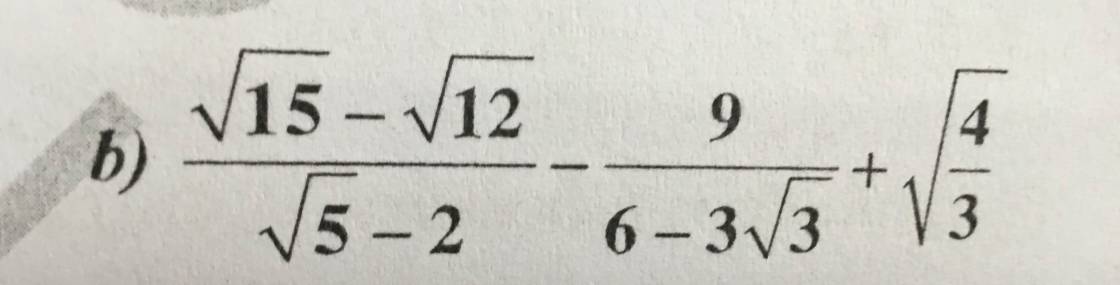Lời giải:
ĐKXĐ: $x\geq 2$
Đặt $\sqrt{x+1}=a; \sqrt{x-2}=b(a,b\geq 0)$ thì:
$a+b+2ab=3a^2-5b^2$
$\Leftrightarrow (3a^2-5b^2-2ab)-(a+b)=0$
$\Leftrightarrow (a+b)(3a-5b)-(a+b)=0$
$\Leftrightarrow (a+b)(3a-5b-1)=0$
Nếu $a+b=0$ thì do $a\geq 0, b\geq 0$ nên $a=b=0$
$\Leftrightarrow \sqrt{x+1}=\sqrt{x-2}=0$ (loại)
Nếu $3a-5b-1=0$
$\Leftrightarrow 3\sqrt{x+1}-5\sqrt{x-2}=1$
\(\Leftrightarrow 3\sqrt{x+1}=5\sqrt{x-2}+1\)
$\Leftrightarrow 3(\sqrt{x+1}-2)=5(\sqrt{x-2}-1)$
$\Leftrightarrow \frac{3(x-3)}{\sqrt{x+1}+2}=\frac{5(x-3)}{\sqrt{x-2}+1}$
$\Rightarrow x=3$ hoặc $\frac{3}{\sqrt{x+1}+2}=\frac{5}{\sqrt{x-2}+1}(*)$
Dễ thấy ở TH $(*)$ thì vt < vp nên $x=3$ là nghiệm duy nhất của pt.