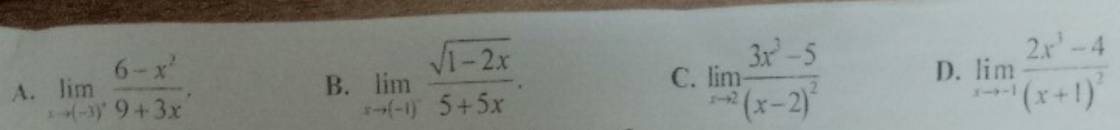1.
Câu này chắc người ra đề nhầm lẫn, vì giới hạn đã cho không tồn tại (giới hạn phải tại 1 bằng dương vô cực, giới hạn trái tại 1 bằng âm vô cực nên ko tồn tại giới hạn tại 1)
Nếu đề là \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[]{2x-1}\sqrt[3]{3x-2}-1}{x-1}\) thì tính được
2.
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[]{2x-3}.\sqrt[3]{5x-2}-2}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{5x-2}\left(\sqrt[]{2x-3}-1\right)+\sqrt[3]{5x-2}-2}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{\sqrt[3]{5x-2}\left(2x-4\right)}{\sqrt[]{2x-3}+1}+\dfrac{5x-10}{\sqrt[3]{\left(5x-2\right)^3}+2\sqrt[3]{5x-2}+4}}{x-2}\)
\(=\lim\limits_{x\rightarrow2}\left(\dfrac{2\sqrt[3]{5x-2}}{\sqrt[]{2x-3}+1}+\dfrac{5}{\sqrt[3]{\left(5x-3\right)^2}+2\sqrt[3]{5x-3}+4}\right)\)
\(=\dfrac{2.2}{1+1}+\dfrac{5}{4+4+4}=...\)
Câu 3 đề bài phạm sai lầm y như câu 1