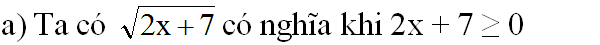Question

Tìm x để mỗi căn thức sau có nghĩa:

a. \(\sqrt{2x+7};\)       b. \(\sqrt{-3x+4};\)          c. \(\sqrt{\dfrac{1}{-1+x}};\)       d. \(\sqrt{1+x^2}.\)

Answer 1

Answer 2

a) \(\sqrt{2x+7}\)

Để \(\sqrt{2x+7}\) có nghĩa\(\Leftrightarrow\)2x+7\(\ge\)0

\(\Leftrightarrow\)2x\(\ge\)-7

\(\Leftrightarrow\)x\(\ge\)\(\dfrac{-7}{2}\)

b) \(\sqrt{-3x+4}\)

Để \(\sqrt{-3x+4}\) có nghĩa \(\Leftrightarrow\)-3x+4\(\ge\)0

\(\Leftrightarrow\)-3x\(\ge\)-4

\(\Leftrightarrow\)x\(\le\)\(\dfrac{4}{3}\)

c)\(\sqrt{\dfrac{1}{-1+x}}\)

Để \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa \(\Leftrightarrow\)\(\dfrac{1}{-1+x}\ge0\)

\(\Leftrightarrow\)-1+x>0

\(\Leftrightarrow\)x>1

d) \(\sqrt{1+x^2}\)

Ta có x²+1\(\ge\)1>0;\(\forall\)x\(\in R\)

Vậy x\(\in R\)

Answer 3

a) \(\sqrt{2x+7}\) có nghĩa khi \(2x+7\ge0\) \(\Leftrightarrow\) \(2x\ge-7\) \(\Leftrightarrow\) \(x\ge\dfrac{-7}{2}\)

b) \(\sqrt{-3x+4}\) có nghĩa khi \(-3x+4\ge0\) \(\Leftrightarrow\) \(-3x\ge-4\) \(\Leftrightarrow\) \(x\le\dfrac{4}{3}\)

c) \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi \(\dfrac{1}{-1+x}>0\) \(\Leftrightarrow\) \(-1+x>0\) \(\Leftrightarrow\) \(x>1\)

\(\sqrt{1+x^2}\) ta có \(1+x^2>0\forall x\) \(\Rightarrow\) căn thức luôn có nghĩa\(\forall x\)

Answer 4

a.\(\sqrt{2x+7}\) có nghĩa khi 2x+7\(\ge\) 0\(\Leftrightarrow\) 2x\(\ge\) -7

\(\Leftrightarrow x\ge-\dfrac{7}{2}\)

b.\(\sqrt{-3x+4}\) có nghĩa khi \(-3x+4\ge0\Leftrightarrow-3x\ge-4\Leftrightarrow x\le\dfrac{4}{3}\)

c.\(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi\(\dfrac{1}{-1+x}>0\Leftrightarrow-1+x>0\Leftrightarrow x>1\)

d.\(\sqrt{1+x^2}\) có nghĩa khi\(1+x^2\ge0\) (với mọi x)\(\Leftrightarrow x\in R\)