Đặt \(x^2=a\ge0\).
PT đã cho trở thành: \(a^2+a+1=y^2\).
Ta có: \(a^2< a^2+a+1\le a^2+2a+1=\left(a+1\right)^2\).
Mà \(a^2+a+1=y^2\) là số chính phương nên theo nguyên lí kẹp ta có \(a^2+a+1=\left(a+1\right)^2\Leftrightarrow a=0\Rightarrow x=0;y=1\).
cho hệ phương trinh {x+y=2
{x+my=4
a)giải hệ phương trình khi m=1
b) tìm m để có nghiểm duy nhất (x,y) thỏa mãn x+y=2
1) Chứng minh rằng: \(x^3-7y=51\) không có nghiệm nguyên
2) Tìm nghiệm nguyên của phương trình \(x^2-5y^2=27\)
3) Tìm nghiệm nguyên dương
a) \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\)
b)\(\dfrac{1}{x}+\dfrac{1}{y}=z\)
a) tìm số tự nhiên x và số nguyên y thỏa mãn: \(x^2y+2xy+x^2-2018x+y=-1\)
b) giải hệ phương trình \(\left\{{}\begin{matrix}x^2-2y^2+xy=2y-2x\\\sqrt{x+2y+1}+\sqrt{x^2+y+2}=4\end{matrix}\right.\)
1. Tìm nghiệm nguyên của phương trình xy-x+y=4
giải phương trinh \(x^2-5x+14=4\sqrt{x+1}\)
Tìm nghiệm nguyên không âm thỏa mãn phương trình: x^2=y^2 + căn y+1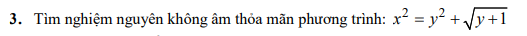
tìm nhiệm nguyên của phương trình:
\(1!+2!+...+x!=y^2\)
Tìm nghiệm nguyên của phương trình: \(x^2-25=y.\left(y+6\right)\)
a) Tìm cặp số x,y nguyên dương thỏa mãn \(x^2+y^2\left(x-y+1\right)-\left(x-1\right)y=22\)
b) Tìm các cặp số x,y,z nguyên dương thỏa mãn \(\dfrac{xy+yz+zx}{x+y+z}=4\)
