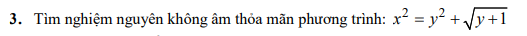Question

tìm nghiệm nguyên của phương trình: (x-1)(y+1)=(x+y)^2

Answer 1

\(xy+x-y-1=x^2+2xy+y^2\)

\(\Leftrightarrow x^2+xy+y^2-x+y+1=0\)

\(\Leftrightarrow2x^2+2xy+2y^2-2x+2y+2=0\)

\(\Leftrightarrow x^2+2xy+y^2+x^2-2x+1+y^2+2y+1=0\)

\(\Leftrightarrow\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\x-1=0\\y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)

Vậy pt đã cho có cặp nghiệm duy nhất \(\left(x;y\right)=\left(1;-1\right)\)