`sqrt{-2x^2+8x-5}`
`=sqrt{-2(x^2-4x+4)+8-5}`
`=sqrt{-2(x-2)^2+3}`
Vì `-2(x-2)^2<=0`
`=>sqrt{-2(x-2)^2+3}<=sqrt3`
Dấu "=" xảy ra khi `x-2=0<=>x=2`
Vậy `GTLN{sqrt{-2x^2+8x-5}}=sqrt3<=>x=2`
`sqrt{-2x^2+8x-5}`
`=sqrt{-2(x^2-4x+4)+8-5}`
`=sqrt{-2(x-2)^2+3}`
Vì `-2(x-2)^2<=0`
`=>sqrt{-2(x-2)^2+3}<=sqrt3`
Dấu "=" xảy ra khi `x-2=0<=>x=2`
Vậy `GTLN{sqrt{-2x^2+8x-5}}=sqrt3<=>x=2`
Tìm GTLN
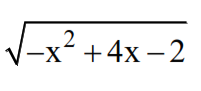
Tìm GTLN của:
\(A=\sqrt{3x-5}+\sqrt{7-3x}\)
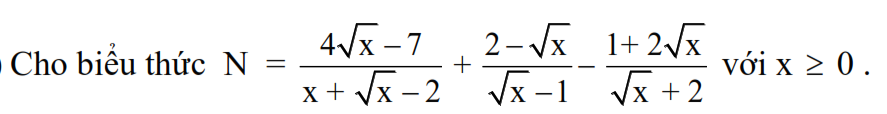
a) Tìm x để N=\(\dfrac{1}{2}\)
b) Tìm x ∈ \(Z\) sao cho N ∈ \(Z\)
c) Tìm GTLN của N
Tìm GTLN của:
\(A=\dfrac{-3\sqrt{x}}{\sqrt{x}+1}\)
Bài 1:
A=\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
a) Tìm tập xác định của biểu thức A
b) Rút gọn biểu thức A
c) Chứng minh rằng A>0 với mọi x≠1
d) Tìm x để A đạt GTLN, tìm GTLN đó
Tìm GTLN của: \(A=\dfrac{\sqrt{x}+1}{2\sqrt{x}+1}\)
Bài 1: tìm GTLN của A= (x+căn(x)+2)/(x-1)
Tìm GTLN của \(A=\sqrt{x-2}+2\sqrt{x+1}+2019-x\)