Để biểu thức đạt giá trị nguyên thì x +3 \(⋮\) 2x-1
=> 2(x+3) \(⋮\)2x-1
=> 2x -1 + 7 \(⋮\) 2x+1
=> 7 \(⋮\) 2x +1 hay 2x+1 là ước của 7
| 2x+1 | 7 | 1 | -1 | -7 |
| x | 3 | 0 | -1 | -4 |
Vậy x \(\in\left\{3;0;-1;-4\right\}\)
Để biểu thức đạt giá trị nguyên thì x +3 \(⋮\) 2x-1
=> 2(x+3) \(⋮\)2x-1
=> 2x -1 + 7 \(⋮\) 2x+1
=> 7 \(⋮\) 2x +1 hay 2x+1 là ước của 7
| 2x+1 | 7 | 1 | -1 | -7 |
| x | 3 | 0 | -1 | -4 |
Vậy x \(\in\left\{3;0;-1;-4\right\}\)
Cho biểu thức:
B = (\(\dfrac{x-2}{2x-2}+\dfrac{3}{2x-2}-\dfrac{x+3}{2x+2}\)) : (\(1-\dfrac{x-3}{x+1}\))
a) Tìm điều kiện của x để giá trị của biểu thức được xác định
b) Tính giá trị của biểu thức B với x = 2005
Cho D=\(\dfrac{2x+4}{3x-1}\) (x ≠ \(\dfrac{1}{3}\)).Tìm x nguyên để D có giá trị nguyên.
mn giúp mik vs ạ!!!
Nếu \(\dfrac{x-y}{z-y}=-10\) ( y khác z). Tính giá trị của biểu thức: \(\dfrac{x-z}{y-z}\)
a. Cho x,y,z là 3 số khác 0 thỏa mãn \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\)
Tính giá trị biểu thức A=\(\dfrac{\left(x+y\right)\left(y+z\right)\left(z+x\right)}{xyz}\)
b. Cho a,b,c là các số hữu tỉ khác nhau từng đôi một. Chứng minh rằng A=\(\dfrac{1}{\left(a-b\right)^2}+\dfrac{1}{\left(b-c\right)^2}+\dfrac{1}{\left(c-a\right)^2}\)
là bình phương của 1 số hữu tỉ
c. Tìm giá trị lớn nhất của biểu thức B=\(\dfrac{5x^2+4x-1}{x^2}\)
tính giá trị của biểu thức x^2-2x-3/x^2+2x+1 với x khác -1 tại 3x-1=0
tìm giá trị lớn nhất của biểu thức (-x^3+8)/(x-2)
Tìm các giá trị của biến số x để phân thức sau bằng không: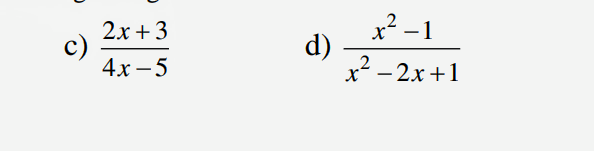
Cho biểu thức: A=\(\frac{x^2-2x+1}{x-1}+\frac{x^2+2x+1}{x+1}-3\)
a)Tìm điều kiện để giá trị của biểu thức A đc xác định
b) Rút gọn biểu thức A
c)Tính giá trị của A khi x=3
d) Tìm x khi A= -2
Tìm điều kiện của x để phân thức sau có ý nghĩa :
a)\(\dfrac{x-2}{x-5}\) b)\(\dfrac{2x-1}{\dfrac{1}{2}x+4}\)c)\(\dfrac{5}{-2x-10}\)