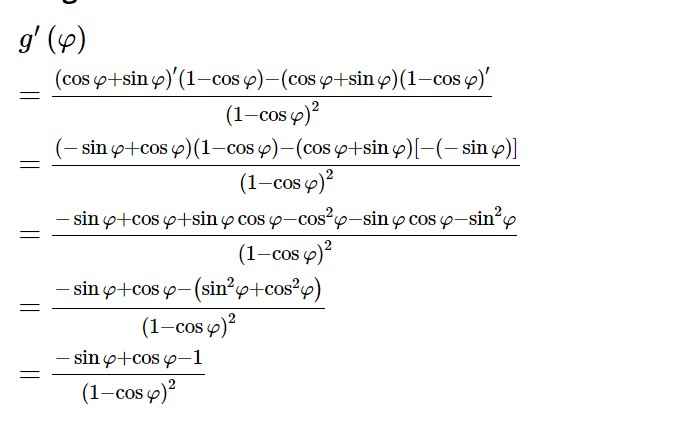Bài 3: Đạo hàm của hàm số lượng giác
Các câu hỏi tương tự
Tính \(\dfrac{f'\left(1\right)}{\varphi'\left(1\right)}\), biết rằng \(f\left(x\right)=x^2\) và \(\varphi\left(x\right)=4x+\sin\dfrac{\pi x}{2}\) ?
Chứng minh rằng các hàm số sau có đạo hàm không phụ thuộc vào x :
a) \(y=\sin^6x+\cos^6x+3\sin^2x.\cos^2x\)
b) \(y=\cos^2\left(\dfrac{\pi}{3}-x\right)+\cos^2\left(\dfrac{\pi}{3}+x\right)+\cos^2\left(\dfrac{2\pi}{3x}-x\right)+\cos^2\left(\dfrac{2\pi}{3x}+x\right)-2\sin^2x\)
Tìm đạo hàm của hàm số sau :
\(y=\sin\left(\cos^2x\right)\cos\left(\sin^2x\right)\)
Tìm đạo hàm của hàm số sau :
\(y=\left(x\sin\alpha+\cos\alpha\right)\left(x\cos\alpha-\sin\alpha\right)\)
Tìm đạo hàm của hàm số :
\(f\left(t\right)=\dfrac{\cos t}{1-\sin t}\) tại \(t=\dfrac{\pi}{6}\)
Tìm đạo hàm của hàm số:
h(x)=\(\cos^2\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\right)\)
Tìm đạo hàm của hàm số sau :
\(y=\dfrac{\sin x-x\cos x}{\cos x+x\sin x}\)
Tìm đạo hàm của hàm số :
\(y=\sin^23x+\dfrac{1}{\cos^2x}\)
Tìm đạo hàm của hàm số :
\(y=\dfrac{2}{\cos\left(\dfrac{\pi}{6}-5x\right)}\)