MNPQ là hình thang cân
=>MP=NQ và MQ=NP
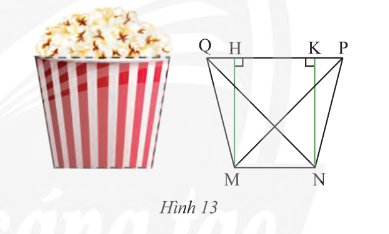
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.
a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)
b) \(\widehat P = \widehat Q = 110^\circ \)
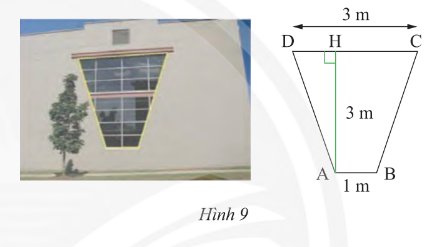
Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.
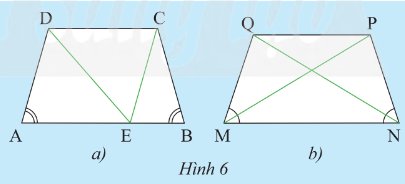
a) Cho hình thang cân \(ABCD\) có hai đáy là \(AB\) và \(CD\) (\(AB > CD\). Qua \(C\) vẽ đường thẳng song song với \(AD\) và cắt \(AB\) tại \(E\) (Hình 6a)
i) Tam giác \(CEB\) là tam giác gì? Vì sao?
ii) So sánh \(AD\) và \(BC\)
b) Cho hình thang cân \(MNPQ\) có hai đáy là \(MN\) và \(PQ\) (Hình 6). So sánh \(MP\) và \(NQ\)
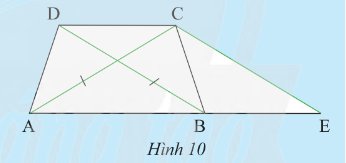
Cho hình thang \(ABCD\) có hai đáy là \(AB\), \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\), song song với \(BD\) và cắt \(AB\) tại \(E\).
a) Tam giác \(CAE\) là tam giác gì? Vì sao?
b) So sánh tam giác \(ABD\) và tam giác \(BAC\)
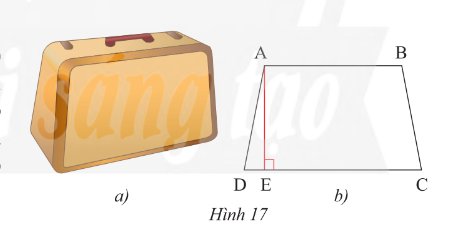
Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là \(60\)cm, cạnh bên là \(61\)cm và đáy lớn là \(92\)cm. Tính độ dài đáy nhỏ.
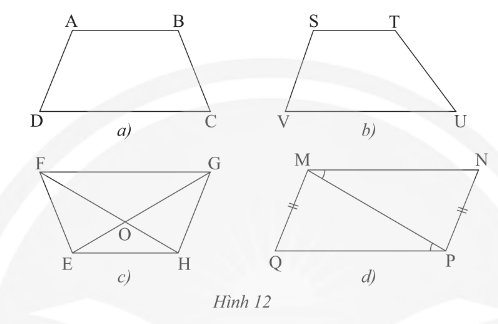
Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12.
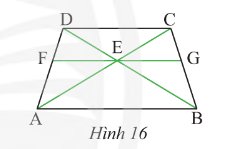
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).
Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo \(\widehat A\) và \(\widehat B\).
