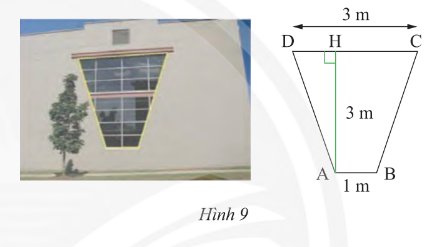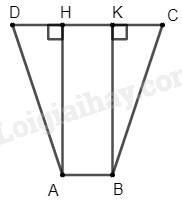
Kẻ đường cao \(BK\)
Suy ra \(AH = BK\) và \(AHKB\) là hình chữ nhật
Suy ra \(HK = AB = 1\)cm
Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AD = BC\) (tc)
Xét \(\Delta AHD\) và \(\Delta BKC\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ \) (gt)
\(\widehat D = \widehat C\) (định nghĩa hình thang cân)
\(AD = BC\) (tính chất hình thang cân)
Suy ra: \(\Delta AHD = \Delta BKC\) (ch – cgv)
Suy ra \(DH = KC\) (hai cạnh tương ứng)
Suy ra \(DH = KC = \frac{{CD - HK}}{2} = \frac{{3 - 1}}{2} = 1\) (cm)
Suy ra \(HC = 2\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(AHD\) ta có:
\(A{D^2} = D{H^2} + A{H^2} = {1^2} + {3^2} = 10\)
Suy ra \(AD = \sqrt {10} \) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(ACH\) ta có:
\(A{C^2} = A{H^2} + H{C^2} = {3^2} + {2^2} = 9 + 4 = 13\)
\(AC = \sqrt {13} \) (cm)
Vậy \(AC = BD = \sqrt {13} \)cm; \(AD = BC = \sqrt {10} \) cm