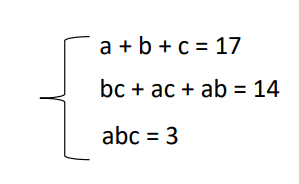Ôn thi vào 10
Các câu hỏi tương tự
Cho các biểu thức B = (sqrt(x))/(sqrt(x) - 1) - (2sqrt(x))/(x - 1)và C = (sqrt(x))/(sqrt(x) + 1) - 1/(x + sqrt(x)) với x > 0 x ne1 .
a) Rút gọn các biểu thức B và C.
b) Tim x de B. C = 1/3 .
c) Chứng minh rằng với x > 0 x ne1 thì tích B.C không thể nhận giá trị nguyên.
16 tháng 5 2021 lúc 15:15
Cho đường tròn (O;R) đường kính AB, lấy M là điểm bất kì thuộc đường tròn khác A,B . Tiếp tuyến tại M cắt 2 tiếp tuyển của A,B lần lượt tại C và D
a)CMR: AOMC và BOMD nội tiếp
b) OC vuông góc OD và AOC = AMC = OBM = ODM
c) Trong trường hợp biết BAM = 60o . Chứng minh △BDM đều và tính diện tích hình quạt tròn chắc cung nhỏ MB của đường tròn theo R
16 tháng 5 2021 lúc 16:28
Cho đường tròn (O;R) đường kính AB, lấy M là điểm bất kì thuộc đường tròn khác A,B . Tiếp tuyến tại M cắt 2 tiếp tuyển của A,B lần lượt tại C và D
a)CMR: AOMC và BOMD nội tiếp
b) OC vuông góc OD và AOC = AMC = OBM = ODM
c) Trong trường hợp biết BAM = 60o . Chứng minh △BDM đều và tính diện tích hình quạt tròn chắc cung nhỏ MB của đường tròn theo R
Từ điểm a nằm ngoài đường (O) vẽ hai tiếp tuyến AB,AC và cát tuyến AEF (B,C là tiếp điểm,tia AF nằm giữa hai tia AB và AO,E nằm giữa A và F).Gọi I là giao điểm của AO và BC K là trung điểm EFa) chứng minh ABOC nội tiếp b) Biết OB3cm,BOC120.tính độ dài cung tròn BEC c) đường thẳng đi qua K song song với BF cắt BC ở M .Chứng minh rằng góc KMC gócKEC d) Tia FM cắt AB tại N .chứng minh N là trung điểm ABlàm câu d hộ mình cái
Đọc tiếp
Từ điểm a nằm ngoài đường (O) vẽ hai tiếp tuyến AB,AC và cát tuyến AEF (B,C là tiếp điểm,tia AF nằm giữa hai tia AB và AO,E nằm giữa A và F).
Gọi I là giao điểm của AO và BC K là trung điểm EF
a) chứng minh ABOC nội tiếp
b) Biết OB=3cm,BOC=120.tính độ dài cung tròn BEC
c) đường thẳng đi qua K song song với BF cắt BC ở M .Chứng minh rằng góc KMC = gócKEC
d) Tia FM cắt AB tại N .chứng minh N là trung điểm AB
làm câu d hộ mình cái 
28 tháng 10 2021 lúc 21:16
Cho \(A=\dfrac{2\sqrt{x}+4}{\sqrt{x}-3}\) và \(B=\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\) (\(x\ge0;x\ne9\))
a, Rút gọn B.
b, Biết \(C=\dfrac{B}{A}\). Tìm \(x\in Z\) để \(C< -\dfrac{1}{3}\).
Cho hai đường tròn (O;13cm) và (O'10cm) cắt nhau tại hai điểm phân biệt A,B. Đoạn OO' cắt (O);(O') lần lượt tại E và F . Biết EF=3cm , độ dài OO' là A.20cm B.18cm C.19cm D.16cm
Giúp mk với ak
Tính thể tích của một hình lăng trụ đứng tam giác đều ABC.A'B'C' biết cạnh đáy AB - a và cạnh bên AA' - \(a\sqrt{3}\)
Bài 4: cho parabol (P) : y ax2 a) Tìm a biết (P) đi qua điểm C( -4;-4). Vẽ (P) với a vừa tìm được và vẽ đường thẳng (d) y dfrac{x}{4}– 3 trên cùng mặt phẳng tọa độ b) Tìm tọa độ điểm của (p) và (d) bằng phép tính
Đọc tiếp
Bài 4: cho parabol (P) : y = ax2
a) Tìm a biết (P) đi qua điểm C( -4;-4). Vẽ (P) với a vừa tìm được và vẽ đường thẳng (d)
y = \(\dfrac{x}{4}\)– 3 trên cùng mặt phẳng tọa độ
b) Tìm tọa độ điểm của (p) và (d) bằng phép tính
Cho ba số nguyên dương a; b và c thỏa mãn (a; b;c) =1 và \(a^2+4b^2+4c^2+7bc=4a.\left(b+c\right)\).
Chứng minh rằng b , c là các số chính phương.
P/s: Nhờ quý thầy cô hỗ trợ và giúp đỡ với ạ! cám ơn nhiều lắm ạ