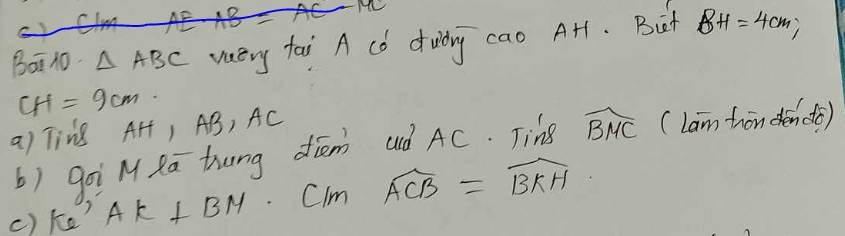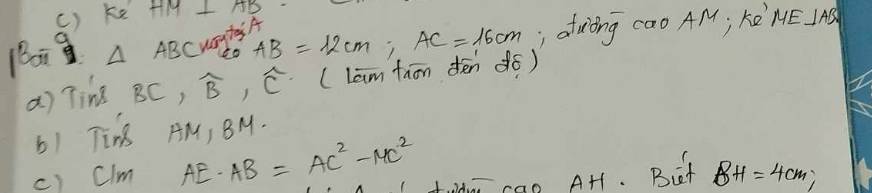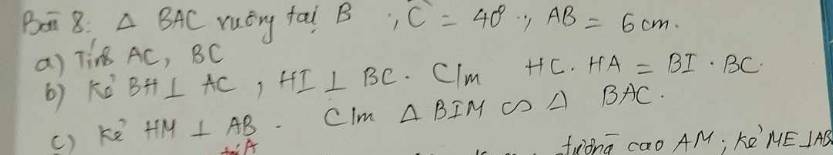a: BC=BH+CH
=4+9
=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=\sqrt{4\cdot9}=6\left(cm\right)\\AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\\AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
b: AM=AC/2=1,5*căn 13(cm)
Xét ΔAMB vuông tại M có
\(\tan AMB=\dfrac{AB}{AM}=\dfrac{2\sqrt{13}}{1.5\sqrt{13}}=\dfrac{4}{3}\)
=>\(\widehat{AMB}\simeq53^0\)
=>\(\widehat{BMC}=180^0-53^0=127^0\)
c: Xét tứ giác AKHB có \(\widehat{AKB}=\widehat{AHB}=90^0\)
nên AKHB là tứ giác nội tiếp
=>\(\widehat{BKH}=\widehat{BAH}\)
mà \(\widehat{BAH}=\widehat{C}\)
nên \(\widehat{BKH}=\widehat{C}\)