§2. Tổng và hiệu của hai vectơ
Các câu hỏi tương tự
| Cho tam giác ABC có trọng tâm G, gọi M, N, P lần lượt là trung điểm của BC, CA, AB |
a) Tìm các vectơ bằng vecto MN b) Dựng điểm I sao cho vecto AG bằng vecto PI
c) Tứ giác BGMI là hình gì ?
Cho mình hỏi : Cho tam giác ABC và A'B'C' có trùng trọng tâm. Chứng minh rằng vec tơ CC' = vec tơ A'B + vec tơ B'A
Gọi vecto GA + GB+GC =veto 0. CMR G là trọng tâm tam giác ABC
Cho hình bình hành ABCD . Gọi M,N là các điểm thỏa vectơ AM =2/3 AD , vectơ = 1/4BC . Gọi G là trọng tâm của tam giác CMN . Phân tích AG theo AB ,AD
Giúp mình với Cho tam giác ABC có G là trọng tâm , I là trung điểm của BC . Chứng minh rằng a) vectơIB+vectơIC=vectơ0 b)vectơGA+vectơGB+vectơGC=vectơ0
tam giác ABC đều cạnh a,dựng hình vuông BCMN.Gọi G là trọng tâm tam giác ABC.Tính theo a độ dài vectơ u=vectơ GA+vectơ GB+vectơ GM+vecto GN
Cho tam giác ABC đều cạnh a, trọng tâm G.Tính 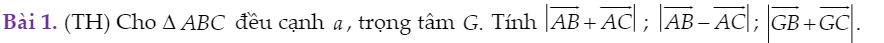
cho tam giác ABC gọi M,N,P lần lượt là trung điểm của BC,CA,AB . chứng minh rằng
BM+CN+AP=0
OA+OB+OC=OM+ON+OP với O bất kì
Cho tam giác ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Tính tổng các vectơ
AM + BN + CP










