Question

Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.

a) Chứng minh \(\widehat {CBI} > \widehat {ACI}\);                                            

b) So sánh IB và IC.

Answer 1

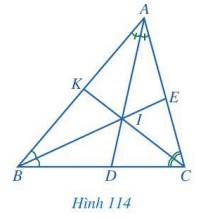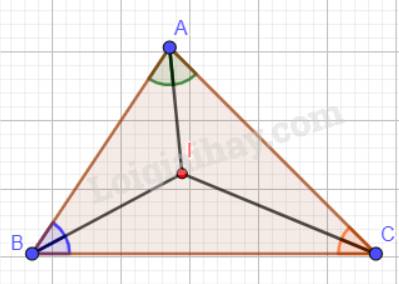
a) Ta có: AB < AC nên \(\widehat {ABC} > \widehat {ACB}\)(góc ABC đối diện với cạnh AC; góc ACB đối diện với cạnh AB).

Mà BI và CI là hai đường phân giác của góc ABC và góc ACB nên: \(\widehat {CBI} > \widehat {ACI}\)

(Vì: \(\widehat {CBI} = \dfrac{1}{2}\widehat {ABC};\widehat {ACI} = \dfrac{1}{2}\widehat {ACB}\)).

b) Ta có: \(\widehat {ACI} = \widehat {BCI}\)

Mà \(\widehat {CBI} > \widehat {ACI}\) ( câu a) 

Do đó \(\widehat {CBI} > \widehat {BCI}\).

Mà IC đối diện với góc CBI; IB đối diện với góc BCI.

Vậy IC > IB (cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn).