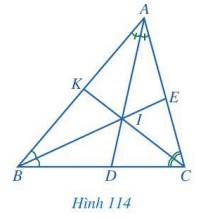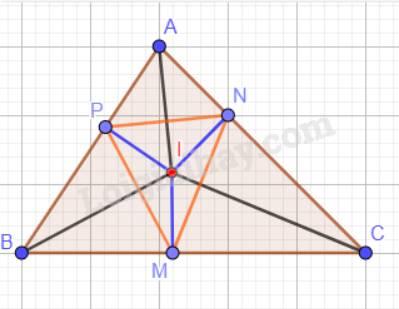
a) Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Vậy các tam giác IMN, INP, IPM có là tam giác cân tại I.
b)
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông). Suy ra: CN = CM ( 2 cạnh tương ứng).
Vậy tam giác CMN có là tam giác cân.
Tương tự, ta có: AP = AN; BP = BM.
Vậy các tam giác ANP, BPM, CMN có là tam giác cân.