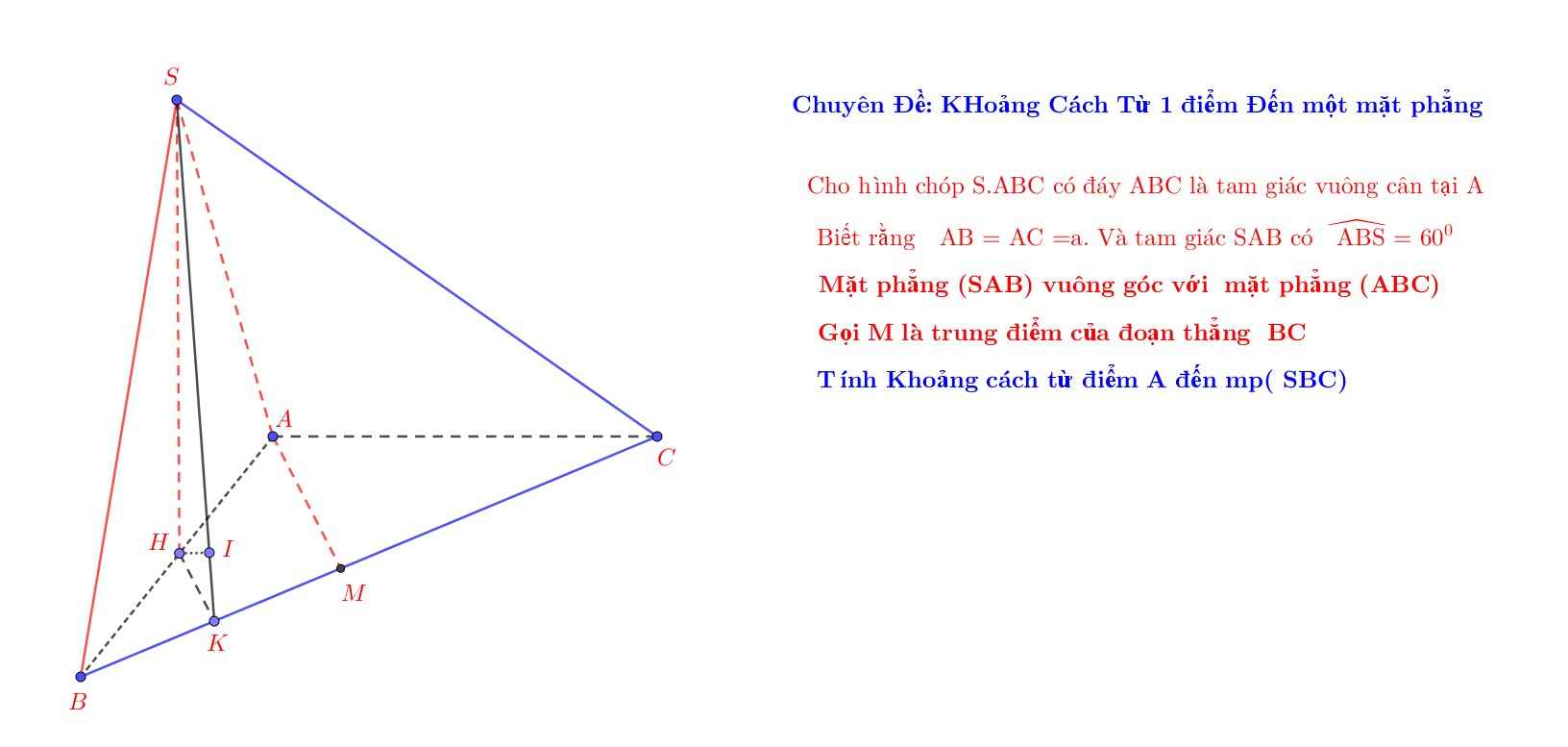
Đề bài thiếu 1 dữ kiện nữa khống chế đỉnh S nên không tính được (ví dụ cần thêm SA hoặc SB hoặc SC gì đó vuông góc (ABC) hay tương tự)
Nếu có thêm dữ kiện \(SA\perp\left(ABC\right)\)
Trong tam giác vuông ABC, kẻ \(AH\perp BC\)
Trong mặt phẳng (SAH), từ A kẻ \(AK\perp SH\)
Ta có: \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
Mà \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\) \(\Rightarrow BC\perp AK\)
\(\left\{{}\begin{matrix}AK\perp BC\\AK\perp SH\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SBC\right)\Rightarrow AK=d\left(A;\left(SBC\right)\right)\)
\(AH=AC.sin\widehat{ACB}=AC.sin60^0=\frac{3a}{2}\)
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC) \(\Rightarrow\widehat{SCA}=60^0\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=3a\)
\(\frac{1}{AK^2}=\frac{1}{SA^2}+\frac{1}{AH^2}\Rightarrow AK=\frac{SA.AH}{\sqrt{SA^2+AH^2}}=\frac{3a\sqrt{5}}{5}\)