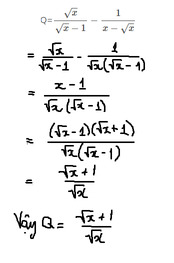\(Q=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\\ =\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}=\dfrac{\sqrt{x}\text{×}\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{x}{x-\sqrt{x}}-\dfrac{1}{x-\sqrt{x}}=\dfrac{x-1}{x-\sqrt{x}}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)