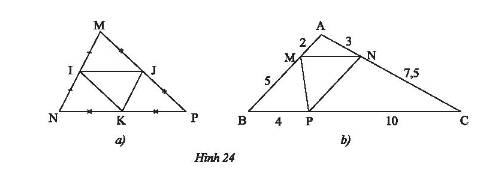
a) Theo hình vẽ ta có:
\(I\) là trung điểm của \(MN\) nên \(IM = IN = \frac{1}{2}MN\);
\(J\) là trung điểm của \(MP\) nên \(JM = JP = \frac{1}{2}MP\);
\(K\) là trung điểm của \(NP\) nên \(KN = KP = \frac{1}{2}NP\).
Xét tam giác \(MNP\) có:
\(\frac{{IM}}{{MN}} = \frac{1}{2};\frac{{MJ}}{{PJ}} = \frac{1}{2} \Rightarrow \frac{{IM}}{{MN}} = \frac{{MJ}}{{PJ}} \Rightarrow IJ//NP\) (Định lí Thales đảo);
\(\frac{{PJ}}{{PM}} = \frac{1}{2};\frac{{PK}}{{PN}} = \frac{1}{2} \Rightarrow \frac{{PJ}}{{PM}} = \frac{{PK}}{{PN}} \Rightarrow JK//MN\) (Định lí Thales đảo);
\(\frac{{NK}}{{NP}} = \frac{1}{2};\frac{{IN}}{{MN}} = \frac{1}{2} \Rightarrow \frac{{NK}}{{NP}} = \frac{{IN}}{{MN}} \Rightarrow IK//MN\) (Định lí Thales đảo).
b) Xét tam giác \(ABC\) có:
\(\frac{{AN}}{{NC}} = \frac{3}{{7,5}} = \frac{2}{5};\frac{{AM}}{{BM}} = \frac{2}{5} \Rightarrow \frac{{AN}}{{NC}} = \frac{{AM}}{{BM}} \Rightarrow MN//BC\)(Định lí Thales đảo);
\(\frac{{CN}}{{AN}} = \frac{{7,5}}{3} = \frac{5}{2};\frac{{CP}}{{PB}} = \frac{{10}}{4} = \frac{5}{2} \Rightarrow \frac{{CN}}{{AN}} = \frac{{CP}}{{BP}} \Rightarrow NP//AB\)(Định lí Thales đảo);
\(\frac{{BM}}{{AM}} = \frac{5}{2};\frac{{PB}}{{CP}} = \frac{4}{{10}} = \frac{2}{5} \Rightarrow \frac{{BM}}{{AM}} \ne \frac{{BP}}{{CP}} \Rightarrow NP\) không song song với \(AB\)(Định lí Thales đảo).