bạn cho thêm dữ kiện đi, chứ như này không đủ đâu Nguyễn Công Thành , mình nghĩ là thêm PQ//NH thì mới đủ chứ!
Bài 2: Định lý đảo và hệ quả của định lý Talet
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
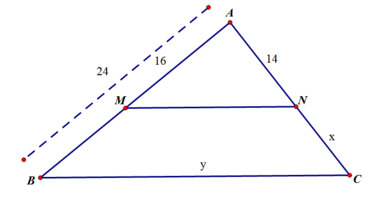
Bài 4: Tìm x trong hình
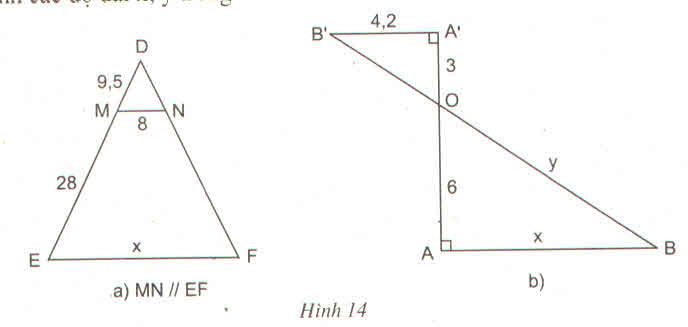
Tính các độ dài \(x,y\) trong hình 14
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không ?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia (h.18). Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB x theo BC a, BC a, BB h
Đọc tiếp
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không ?
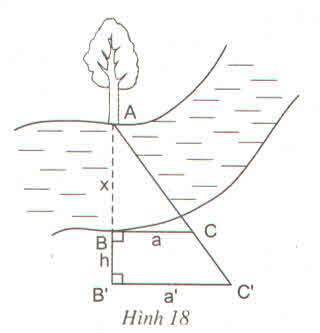
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia (h.18). Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB = x theo BC = a, B'C' = a', BB' = h
Cho ba đoạn thẳng có độ dài là m, n, p (cùng đơn vị đo)
Dự đoạn thẳng có độ dài x sao cho
a) dfrac{x}{m}2
b) dfrac{x}{n}dfrac{2}{3}
c) dfrac{m}{x}dfrac{n}{p}
Hướng dẫn :
Câu b) :
- Vẽ hai tia Ox, Oy
- Trên Ox đặt đoạn thẳng OA 2 đơn vị, OB 3 đơn vị
- Trên tia Oy đặt đoạn thẳng OB n và xác định điểm A sao cho
dfrac{OA}{OB}dfrac{OA}{OB}
- Từ đó ta có OAx
Đọc tiếp
Cho ba đoạn thẳng có độ dài là m, n, p (cùng đơn vị đo)
Dự đoạn thẳng có độ dài x sao cho
a) \(\dfrac{x}{m}=2\)
b) \(\dfrac{x}{n}=\dfrac{2}{3}\)
c) \(\dfrac{m}{x}=\dfrac{n}{p}\)
Hướng dẫn :
Câu b) :
- Vẽ hai tia Ox, Oy
- Trên Ox đặt đoạn thẳng OA = 2 đơn vị, OB = 3 đơn vị
- Trên tia Oy đặt đoạn thẳng OB' = n và xác định điểm A' sao cho
\(\dfrac{OA}{OB}=\dfrac{OA'}{OB'}\)
- Từ đó ta có \(OA'=x\)
B1 : Cho tam giác ABC, lấy điểm O bất kì trong tam giác đó. Vẽ các tia AO,BO,CO cắt BC,AC,AB lần lượt tại P,Q và R
CM: frac{OA}{AP}+frac{OB}{BQ}+frac{OC}{CR}2
B2: Cho tam giác ABC, vẽ trung tuyến AM. Điểm I bất kì trên AM, F là giao điểm của BI và AC. E là giao điểm của CI và AB. Từ M kẻ đường thẳng song song với IC cắt AB tại H và kẻ đường thẳng song song với IB cắt AC tại K
CM a, EF//HK
b, EF//BC
Các bạn giúp mk nha (Có hình càng tốt)
Đọc tiếp
B1 : Cho tam giác ABC, lấy điểm O bất kì trong tam giác đó. Vẽ các tia AO,BO,CO cắt BC,AC,AB lần lượt tại P,Q và R
CM: \(\frac{OA}{AP}+\frac{OB}{BQ}+\frac{OC}{CR}=2\)
B2: Cho tam giác ABC, vẽ trung tuyến AM. Điểm I bất kì trên AM, F là giao điểm của BI và AC. E là giao điểm của CI và AB. Từ M kẻ đường thẳng song song với IC cắt AB tại H và kẻ đường thẳng song song với IB cắt AC tại K
CM a, EF\(//\)HK
b, EF\(//\)BC
Các bạn giúp mk nha (Có hình càng tốt)
Cho hình vuông ABCD, trên tia đối của tia CD lấy điểm M bất kì (CM<CD), vẽ hình vuông CMNP (P nằm giữa B và C), DP cắt BM tại H, MP cắt BD tại K.
a) Chứng minh DH vuông góc BM
b) Tính Q=\(\frac{PC}{BC}+\frac{PH}{DH}+\frac{KP}{MK}\)
C) Chứng minh: MP.MK+DK.BD=DM^2
Cho ABC có ba góc nhọn .Qua điểm D thuộc cạnh AB vẽ đường thẳng song song với BC cắt AC tại E .Gọi H và K là hình chiếu của B và D trên AC.Chứng minh
a)\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
b) BD.AC = CE.AB
c)\(\dfrac{DK}{DE}=\dfrac{BH}{BC}\)
d)\(\dfrac{S_{ADE}}{S_{ABC}}=\dfrac{AD.AE}{AB.AC}\)
Hình 6

Cho biết MN // BC, AB = 25 cm, BC = 45 cm, AM = 16 cm, AN = 10 cm
Tính độ dài x, y của các đoạn thẳng MN, AC ?
Cho hình bình hành ABCD. Vẽ tia Ax cắt đường chéo BD ở I, cắt tia BC ở J , cắt tia CD ở K.
1) Theo định lí Thalès thì tỉ số frac{ID}{IB} bằng với những tỉ số nào? Chứng minh IA^2IJ.IK
2) Hai tỉ số frac{AI}{AJ}và frac{AI}{AK}bằng tỉ số nào trên đường chéo BD? Chứng minh frac{1}{AJ}+frac{1}{AK}frac{1}{AI}
Đọc tiếp
Cho hình bình hành ABCD. Vẽ tia Ax cắt đường chéo BD ở I, cắt tia BC ở J , cắt tia CD ở K.
1) Theo định lí Thalès thì tỉ số \(\frac{ID}{IB}\) bằng với những tỉ số nào? Chứng minh \(IA^2=IJ.IK\)
2) Hai tỉ số \(\frac{AI}{AJ}\)và \(\frac{AI}{AK}\)bằng tỉ số nào trên đường chéo BD? Chứng minh \(\frac{1}{AJ}+\frac{1}{AK}=\frac{1}{AI}\)










